 |
YAARX: Yet Another ARX Toolkit
0.1
|
 |
YAARX: Yet Another ARX Toolkit
0.1
|
Computing an ADD partial difference distribution table (pDDT) for the F-function of block cipher TEA. More...
#include "common.hh"#include "adp-xor3.hh"#include "adp-shift.hh"#include "tea.hh"#include "eadp-tea-f.hh"#include "adp-tea-f-fk.hh"Functions | |
| bool | rsh_condition_is_sat (const uint32_t k, const uint32_t new_da, const uint32_t new_dc) |
| bool | lsh_condition_is_sat (const uint32_t k, const uint32_t new_da, const uint32_t new_db) |
| void | tea_f_add_pddt_i (const uint32_t k, const uint32_t n, const uint32_t lsh_const, const uint32_t rsh_const, gsl_matrix *A[2][2][2][2], gsl_vector *C, uint32_t *da, uint32_t *db, uint32_t *dc, uint32_t *dd, double *p, const double p_thres, std::set< differential_t, struct_comp_diff_dx_dy > *diff_set_dx_dy) |
| void | tea_f_add_pddt (uint32_t n, double p_thres, uint32_t lsh_const, uint32_t rsh_const, std::set< differential_t, struct_comp_diff_dx_dy > *diff_set_dx_dy) |
| void | tea_f_add_pddt_adjust_to_key (uint32_t nrounds, uint32_t npairs, uint32_t key[4], double p_thres, std::set< differential_t, struct_comp_diff_dx_dy > *diff_set_dx_dy) |
| void | tea_f_add_pddt_dxy_to_dp (std::multiset< differential_t, struct_comp_diff_p > *diff_mset_p, const std::set< differential_t, struct_comp_diff_dx_dy > diff_set_dx_dy) |
| void | tea_f_add_pddt_exper (gsl_matrix *A[2][2][2][2], uint32_t n, double p_thres, uint32_t lsh_const, uint32_t rsh_const, std::multiset< differential_t, struct_comp_diff_p > *diff_mset_p) |
| void | tea_f_add_pddt_fk_exper (uint32_t n, double p_thres, uint32_t delta, uint32_t k0, uint32_t k1, uint32_t lsh_const, uint32_t rsh_const, std::multiset< differential_t, struct_comp_diff_p > *diff_mset_p) |
| bool | is_dx_in_set_dx_dy (uint32_t dy, uint32_t dx_prev, std::set< differential_t, struct_comp_diff_dx_dy > diff_set_dx_dy) |
| bool | is_dx_in_set_dx_dy_mask_i (uint32_t mask_i, const uint32_t dy, const uint32_t dx_prev, std::set< differential_t, struct_comp_diff_dx_dy > diff_set_dx_dy) |
| void | tea_f_da_db_dc_add_pddt_i (const uint32_t k, const uint32_t n, const uint32_t lsh_const, const uint32_t rsh_const, gsl_matrix *A[2][2][2][2], gsl_vector *C, const uint32_t da, const uint32_t db, const uint32_t dc, uint32_t *dd, double *p, const double p_thres, uint32_t da_prev, std::set< differential_t, struct_comp_diff_dx_dy > *hways_diff_set_dx_dy, std::multiset< differential_t, struct_comp_diff_p > *hways_diff_mset_p, std::set< differential_t, struct_comp_diff_dx_dy > *diff_set_dx_dy, std::multiset< differential_t, struct_comp_diff_p > *diff_mset_p, uint32_t *cnt_new) |
| uint32_t | tea_f_da_add_pddt (uint32_t n, double p_thres, uint32_t lsh_const, uint32_t rsh_const, const uint32_t da, const uint32_t da_prev, std::set< differential_t, struct_comp_diff_dx_dy > *hways_diff_set_dx_dy, std::multiset< differential_t, struct_comp_diff_p > *hways_diff_mset_p, std::set< differential_t, struct_comp_diff_dx_dy > *diff_set_dx_dy, std::multiset< differential_t, struct_comp_diff_p > *diff_mset_p) |
Computing an ADD partial difference distribution table (pDDT) for the F-function of block cipher TEA.
| bool is_dx_in_set_dx_dy | ( | uint32_t | dy, |
| uint32_t | dx_prev, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > | diff_set_dx_dy | ||
| ) |
For a given difference dx, check if in the list of differentials set_dx_dy exists an entry (dx -> dy)
| bool is_dx_in_set_dx_dy_mask_i | ( | uint32_t | mask_i, |
| const uint32_t | dy, | ||
| const uint32_t | dx_prev, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > | diff_set_dx_dy | ||
| ) |
Same as is_dx_in_set_dx_dy but on the mask_i LSBs .
| bool lsh_condition_is_sat | ( | const uint32_t | k, |
| const uint32_t | new_da, | ||
| const uint32_t | new_db | ||
| ) |
Check if two differences 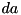 and
and 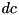 , partially constructed up to bit
, partially constructed up to bit 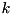 (WORD_SIZE
(WORD_SIZE 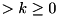 ), are valid input and output difference respectively, for the LSH operation.
), are valid input and output difference respectively, for the LSH operation.
| k | bit position: WORD_SIZE 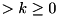 . . |
| new_da | input difference to LSH partially constructed up to bit 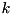 . . |
| new_db | output difference from LSH partially constructed up to bit 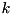 . . |
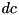 , after being fully constructed, will be a valid output difference from LSH, given the input difference
, after being fully constructed, will be a valid output difference from LSH, given the input difference 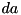 ; FALSE otherwise.
; FALSE otherwise.More Details:
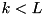 : check if
: check if ![$db[k:0] = 0$](form_412.png) .
.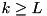 : check if
: check if ![$(db \gg L)[n-(k-L+1):0] = da[n-(k-L+1):0]$](form_414.png) .
.where 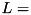 TEA_LSH_CONST,
TEA_LSH_CONST, 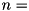 WORD_SIZE.
WORD_SIZE.
| bool rsh_condition_is_sat | ( | const uint32_t | k, |
| const uint32_t | new_da, | ||
| const uint32_t | new_dc | ||
| ) |
Check if two differences 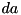 and
and 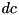 , partially constructed up to bit
, partially constructed up to bit 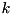 (WORD_SIZE
(WORD_SIZE 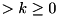 ), are valid input and output difference respectively, for the RSH operation. From the partial information for
), are valid input and output difference respectively, for the RSH operation. From the partial information for 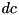 , the algorithm estimates if
, the algorithm estimates if 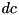 belongs to one of the four possible differences after the RSH operation (see adp_rsh):
belongs to one of the four possible differences after the RSH operation (see adp_rsh): 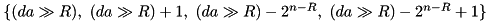 , where
, where 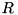 is the RSH constant (TEA_RSH_CONST).
is the RSH constant (TEA_RSH_CONST).
| k | bit position: WORD_SIZE 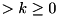 . . |
| new_da | input difference to RSH partially constructed up to bit 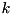 . . |
| new_dc | output difference from RSH partially constructed up to bit 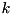 . . |
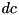 , after being fully constructed, will be a valid output difference from RSH, given the input difference
, after being fully constructed, will be a valid output difference from RSH, given the input difference 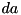 ; FALSE otherwise.
; FALSE otherwise.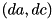 which pass the checks are valid, but there also exist valid differences that do not pass the checks. The reason is that it is hard to detect all valid differences before they have been fully constructed.
which pass the checks are valid, but there also exist valid differences that do not pass the checks. The reason is that it is hard to detect all valid differences before they have been fully constructed.More Details:
Given are two differences 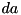 and
and 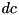 , that are only partially constructed up to bit
, that are only partially constructed up to bit 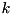 (counting from the LSB
(counting from the LSB 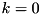 ). rsh_condition_is_sat performs checks on
). rsh_condition_is_sat performs checks on 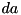 and
and 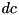 and outputs if
and outputs if 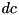 is such that
is such that 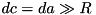 , where
, where 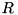 = TEA_RSH_CONST. The idea is to be able to discard pairs of diferences
= TEA_RSH_CONST. The idea is to be able to discard pairs of diferences 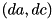 before they have been fully constructed. This allows to more efficiently constrct a list of valid differentials for the TEA F-function recursively. We use these conditions in tea_f_add_pddt_i to discard invalid entries early in the recursion.
before they have been fully constructed. This allows to more efficiently constrct a list of valid differentials for the TEA F-function recursively. We use these conditions in tea_f_add_pddt_i to discard invalid entries early in the recursion.
To perform the checks, the following relations are used:
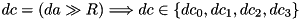 where:
where:
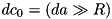 .
.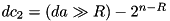 .
.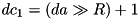 .
.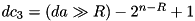 .
.Depending on the bit position 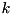 (some of) the following checks are performed:
(some of) the following checks are performed:
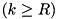 perform check on the
perform check on the 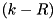 LS bits. If
LS bits. If 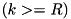 we check if the first
we check if the first 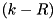 LSB bits of
LSB bits of 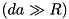 are equal to the first
are equal to the first 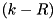 bits of
bits of 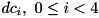 according to the above equations. So we check if any of the following four equations hold:
according to the above equations. So we check if any of the following four equations hold:![$(da \gg R)[0:(k - R)] = (dc_0)[0:(k - R)]$](form_398.png) .
.![$(da \gg R)[0:(k - R)] = (dc_0 + 2^{n-R})[0:(k - R)]$](form_399.png) .
.![$(da \gg R)[0:(k - R)] = (dc_0 - 1)[0:(k - R)]$](form_400.png) .
.![$(da \gg R)[0:(k - R)] = (dc_0 + 2^{n-R} - 1)[0:(k - R)]$](form_401.png) .
.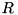 LS bits of
LS bits of 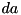 are not zero
are not zero ![$da[(r-1):0] \neq 0$](form_402.png) .
.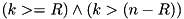 check the
check the 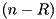 MS bits. When
MS bits. When 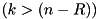 ,
, ![$(da \gg R)[k] = 0$](form_406.png) and we check the top
and we check the top 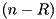 MS bits of
MS bits of 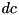 . More specifically, we check if the initial four equations hold for the
. More specifically, we check if the initial four equations hold for the 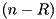 MS bits of the operands:
MS bits of the operands:![$dc_0[(n-1):(n-R+1)] = (da \gg R)[(n-1):(n-R+1)]$](form_407.png) .
.![$dc_1[(n-1):(n-R+1)] = ((da \gg R) + 1)[(n-1):(n-R+1)]$](form_408.png) .
.![$dc_2[(n-1):(n-R+1)] = ((da \gg R) - 2^{n-R})[(n-1):(n-R+1)]$](form_409.png) .
.![$dc_3[(n-1):(n-R+1)] = ((da \gg R) - 2^{n-R} + 1)[(n-1):(n-R+1)]$](form_410.png) .
. | void tea_f_add_pddt | ( | uint32_t | n, |
| double | p_thres, | ||
| uint32_t | lsh_const, | ||
| uint32_t | rsh_const, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | diff_set_dx_dy | ||
| ) |
Compute a partial DDT (pDDT) for the TEA F-function: wrapper function of tea_f_add_pddt_i . By definition a pDDT contains only differentials that have probability above a fixed probability thershold.
| n | word size (default is WORD_SIZE). |
| p_thres | probability threshold (default is TEA_ADD_P_THRES). |
| lsh_const | LSH constant (TEA_LSH_CONST). |
| rsh_const | RSH constant (TEA_RSH_CONST). |
| diff_set_dx_dy | set of differentials  in the pDDT ordered by index in the pDDT ordered by index 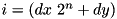 ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. |
| void tea_f_add_pddt_adjust_to_key | ( | uint32_t | nrounds, |
| uint32_t | npairs, | ||
| uint32_t | key[4], | ||
| double | p_thres, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | diff_set_dx_dy | ||
| ) |
Adjust the probabailities of the differentials in a pDDT computed with tea_f_add_pddt , to the value of a fixed key by performing one-round TEA encryptions over a number of chosen plaintext pairs drawn uniformly at random.
| void tea_f_add_pddt_dxy_to_dp | ( | std::multiset< differential_t, struct_comp_diff_p > * | diff_mset_p, |
| const std::set< differential_t, struct_comp_diff_dx_dy > | diff_set_dx_dy | ||
| ) |
From a pDDT represented in the form of a set of differentials ordered by index, compute a pDDT as a set of differentials ordered by probability.
| diff_mset_p | output pDDT: set of differentials  ordered by probability; stored in an STL multiset structure, internally implemented as a Red-Black binary search tree. ordered by probability; stored in an STL multiset structure, internally implemented as a Red-Black binary search tree. |
| diff_set_dx_dy | input pDDT: set of differentials  ordered by index ordered by index 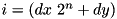 ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. |
| void tea_f_add_pddt_exper | ( | gsl_matrix * | A[2][2][2][2], |
| uint32_t | n, | ||
| double | p_thres, | ||
| uint32_t | lsh_const, | ||
| uint32_t | rsh_const, | ||
| std::multiset< differential_t, struct_comp_diff_p > * | diff_mset_p | ||
| ) |
Experimentally compute the full DDT of the TEA F-function containining expected probabilities, averaged over all keys and round constants. An exhautive search is performed over all input and output differences. Complexity: 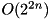 .
.
| A | transition probability matrices for  (adp_xor3_sf). (adp_xor3_sf). |
| n | word size (default is WORD_SIZE). |
| p_thres | probability threshold (default is TEA_ADD_P_THRES). |
| lsh_const | LSH constant (TEA_LSH_CONST). |
| rsh_const | RSH constant (TEA_RSH_CONST). |
| diff_mset_p | set of differentials  ordered by probability (the DDT). ordered by probability (the DDT). |
| void tea_f_add_pddt_fk_exper | ( | uint32_t | n, |
| double | p_thres, | ||
| uint32_t | delta, | ||
| uint32_t | k0, | ||
| uint32_t | k1, | ||
| uint32_t | lsh_const, | ||
| uint32_t | rsh_const, | ||
| std::multiset< differential_t, struct_comp_diff_p > * | diff_mset_p | ||
| ) |
Experimentally compute the full DDT of the TEA F-function containining probabilities for a fixed key and round constant. An exhautive search is performed over all input and output differences. Complexity: 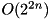 .
.
| n | word size (default is WORD_SIZE). |
| p_thres | probability threshold (default is TEA_ADD_P_THRES). |
| delta | round constant. |
| k0 | first round key. |
| k1 | second round key. |
| lsh_const | LSH constant (TEA_LSH_CONST). |
| rsh_const | RSH constant (TEA_RSH_CONST). |
| diff_mset_p | set of differentials  ordered by probability (the DDT). ordered by probability (the DDT). |
| void tea_f_add_pddt_i | ( | const uint32_t | k, |
| const uint32_t | n, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const, | ||
| gsl_matrix * | A[2][2][2][2], | ||
| gsl_vector * | C, | ||
| uint32_t * | da, | ||
| uint32_t * | db, | ||
| uint32_t * | dc, | ||
| uint32_t * | dd, | ||
| double * | p, | ||
| const double | p_thres, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | diff_set_dx_dy | ||
| ) |
Computes a partial difference distribution table (pDDT) for the F-function of block cipher TEA.
| k | current bit position in the recursion. |
| n | word size (default is WORD_SIZE). |
| lsh_const | LSH constant (default is 4). |
| rsh_const | RSH constant (default is 5). |
| A | transition probability matrices for  (adp_xor3_sf). (adp_xor3_sf). |
| C | unit column vector for computing 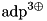 (adp_xor3). (adp_xor3). |
| da | first input difference to the XOR operation in F. |
| db | second input difference to the XOR operation in F. |
| dc | third input difference to the XOR operation in F. |
| dd | output difference from the XOR operation in F. |
| p | probability of the partially constructed differential ![$(da[k:0], db[k:0], dc[k:0] \rightarrow dd[k:0])$](form_181.png) . . |
| p_thres | probability threshold (default is TEA_ADD_P_THRES). |
| diff_set_dx_dy | set of differentials  in the pDDT ordered by index in the pDDT ordered by index 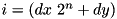 ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. |
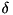 and therefore contains average (as opposed to fixed-key fixed-constants adp_f_fk) probabilities.
and therefore contains average (as opposed to fixed-key fixed-constants adp_f_fk) probabilities.Algorithm Outline:
Applies conceptually the same logic as adp_xor_pddt_i. It recursively constructs all differentials for the XOR operation with three inputs 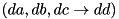 , with the additional requirement that they must satisfy the following properties:
, with the additional requirement that they must satisfy the following properties:
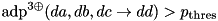 .
.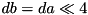 .
.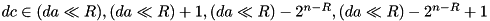 , so that
, so that 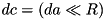 where
where 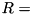 TEA_RSH_CONST.
TEA_RSH_CONST.Only the entries for which 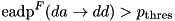 are stored.
are stored.
| uint32_t tea_f_da_add_pddt | ( | uint32_t | n, |
| double | p_thres, | ||
| uint32_t | lsh_const, | ||
| uint32_t | rsh_const, | ||
| const uint32_t | da, | ||
| const uint32_t | da_prev, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | hways_diff_set_dx_dy, | ||
| std::multiset< differential_t, struct_comp_diff_p > * | hways_diff_mset_p, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | diff_set_dx_dy, | ||
| std::multiset< differential_t, struct_comp_diff_p > * | diff_mset_p | ||
| ) |
Wrapper for tea_f_da_db_dc_add_pddt_i . Returns the number of new entries that were added .
| n | word size (default is WORD_SIZE). |
| p_thres | probability threshold (default is TEA_ADD_P_THRES). |
| lsh_const | LSH constant (default is TEA_LSH_CONST). |
| rsh_const | RSH constant (default is TEA_RSH_CONST). |
| da | input difference to F. |
| da_prev | input difference to the previous round. |
| hways_diff_set_dx_dy | set of differentials 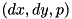 (Highways) ordered by index (Highways) ordered by index 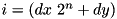 . . |
| hways_diff_mset_p | set of differentials 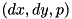 (Highways) ordered by probability p. (Highways) ordered by probability p. |
| diff_set_dx_dy | set of differentials 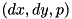 (Countryroads) ordered by index (Countryroads) ordered by index 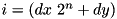 . . |
| diff_mset_p | temporrary set of differentials 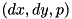 (Countryroads) ordered by probability p. (Countryroads) ordered by probability p. |
diff_set_dx_dy . | void tea_f_da_db_dc_add_pddt_i | ( | const uint32_t | k, |
| const uint32_t | n, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const, | ||
| gsl_matrix * | A[2][2][2][2], | ||
| gsl_vector * | C, | ||
| const uint32_t | da, | ||
| const uint32_t | db, | ||
| const uint32_t | dc, | ||
| uint32_t * | dd, | ||
| double * | p, | ||
| const double | p_thres, | ||
| uint32_t | da_prev, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | hways_diff_set_dx_dy, | ||
| std::multiset< differential_t, struct_comp_diff_p > * | hways_diff_mset_p, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | diff_set_dx_dy, | ||
| std::multiset< differential_t, struct_comp_diff_p > * | diff_mset_p, | ||
| uint32_t * | cnt_new | ||
| ) |
| k | current bit position in the recursion. |
| n | word size (default is WORD_SIZE). |
| lsh_const | LSH constant (default is 4). |
| rsh_const | RSH constant (default is 5). |
| A | transition probability matrices for  (adp_xor3_sf). (adp_xor3_sf). |
| C | unit column vector for computing 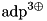 (adp_xor3). (adp_xor3). |
| da | first input difference to the XOR operation in F. |
| db | second input difference to the XOR operation in F. |
| dc | third input difference to the XOR operation in F. |
| dd | output difference from the XOR operation in F. |
| p | probability of the partially constructed differential ![$(da[k:0], db[k:0], dc[k:0] \rightarrow dd[k:0])$](form_181.png) . . |
| p_thres | probability threshold (default is TEA_ADD_P_THRES). |
| da_prev | input difference to the previous round. |
| hways_diff_mset_p | set of differentials 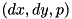 (Highways) ordered by probability p. (Highways) ordered by probability p. |
| hways_diff_set_dx_dy | set of differentials 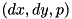 (Highways) ordered by index (Highways) ordered by index 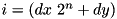 . . |
| diff_mset_p | temporrary set of differentials 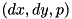 (Countryroads) ordered by probability p. (Countryroads) ordered by probability p. |
| diff_set_dx_dy | set of differentials 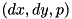 (Countryroads) ordered by index (Countryroads) ordered by index 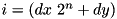 . . |
| cnt_new | number of output differences that were added . |
For a fixed input difference 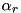 to round
to round 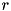 compute a list of output differences
compute a list of output differences 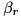 that satisfy the following conditions:
that satisfy the following conditions:
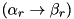 is bigger than a pre-defined threshold
is bigger than a pre-defined threshold p_thres .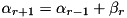 to the next round has a matching entry in the pre-computed pDDT
to the next round has a matching entry in the pre-computed pDDT hways_diff_set_dx_dy.