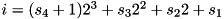Header file for adp-xor3.cc:
More...
Go to the source code of this file.
|
| void | adp_xor3_alloc_matrices (gsl_matrix *A[2][2][2][2]) |
| |
| void | adp_xor3_free_matrices (gsl_matrix *A[2][2][2][2]) |
| |
| void | adp_xor3_print_matrices (gsl_matrix *A[2][2][2][2]) |
| |
| void | adp_xor3_print_matrices_sage (gsl_matrix *A[2][2][2][2]) |
| |
| void | adp_xor3_normalize_matrices (gsl_matrix *A[2][2][2][2]) |
| |
| int | adp_xor3_states_to_index (int s1, int s2, int s3, int s4) |
| |
| void | adp_xor3_sf (gsl_matrix *A[2][2][2][2]) |
| |
| double | adp_xor3 (gsl_matrix *A[2][2][2][2], uint32_t da, uint32_t db, uint32_t dc, uint32_t dd) |
| |
| double | adp_xor3_exper (const uint32_t da, const uint32_t db, const uint32_t dc, const uint32_t dd) |
| |
| #define ADP_XOR3_COLSUM 8 |
Sum of non-zero elements in one column of the  matrices.
matrices.
| #define ADP_XOR3_ISTATE 8 |
Initial state for computing the  S-function.
S-function.
| #define ADP_XOR3_MSIZE 16 |
Number of state values in the  S-functions.
S-functions.
| #define ADP_XOR3_NINPUTS 3 |
Number of inputs to the  operation.
operation.
| #define ADP_XOR3_NMATRIX 16 |
Number of  matrices.
matrices.
Normalization factor for the  matrices.
matrices.
| double adp_xor3 |
( |
gsl_matrix * |
A[2][2][2][2], |
|
|
uint32_t |
da, |
|
|
uint32_t |
db, |
|
|
uint32_t |
dc, |
|
|
uint32_t |
dd |
|
) |
| |
| void adp_xor3_alloc_matrices |
( |
gsl_matrix * |
A[2][2][2][2] | ) |
|
Allocate memory for the transition probability matrices for  .
.
- Parameters
-
| A | transition probability matrices for  . . |
- See Also
- adp_xor3_free_matrices
| double adp_xor3_exper |
( |
const uint32_t |
da, |
|
|
const uint32_t |
db, |
|
|
const uint32_t |
dc, |
|
|
const uint32_t |
dd |
|
) |
| |
| void adp_xor3_free_matrices |
( |
gsl_matrix * |
A[2][2][2][2] | ) |
|
Free memory reserved by a previous call to adp_xor3_alloc_matrices.
- Parameters
-
| A | transition probability matrices for  . . |
| void adp_xor3_normalize_matrices |
( |
gsl_matrix * |
A[2][2][2][2] | ) |
|
Transform the elements of A into probabilities.
- Parameters
-
| A | transition probability matrices for  . . |
| void adp_xor3_print_matrices |
( |
gsl_matrix * |
A[2][2][2][2] | ) |
|
Print the matrices for  .
.
- Parameters
-
| A | transition probability matrices for  . . |
| void adp_xor3_print_matrices_sage |
( |
gsl_matrix * |
A[2][2][2][2] | ) |
|
Print the matrices for  in a format readable by the computer algebra system Sage (http://www.sagemath.org/).
in a format readable by the computer algebra system Sage (http://www.sagemath.org/).
- Parameters
-
| A | transition probability matrices for  . . |
| void adp_xor3_sf |
( |
gsl_matrix * |
A[2][2][2][2] | ) |
|
| int adp_xor3_states_to_index |
( |
int |
s1, |
|
|
int |
s2, |
|
|
int |
s3, |
|
|
int |
s4 |
|
) |
| |
Transform the values of the four states of the S-function for  (adp_xor3_sf) into an index.
(adp_xor3_sf) into an index.
- Parameters
-
| s1 | state corresponding to the first input difference. |
| s2 | state corresponding to the second input difference. |
| s3 | state corresponding to the third input difference. |
| s4 | state corresponding to the output difference. |
- Returns
- the index
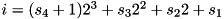


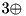 matrices.
matrices.  S-function.
S-function.  S-functions.
S-functions. 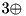 operation.
operation.  matrices.
matrices.  matrices.
matrices.  . Complexity:
. Complexity: 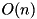 .
. computed with adp_xor3_sf.
computed with adp_xor3_sf. 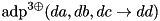 .
.  .
.  .
.  computed experimentally over all inputs. Complexity:
computed experimentally over all inputs. Complexity: 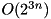 .
.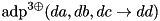 .
.  .
.  .
.  .
.  .
.  in a format readable by the computer algebra system Sage (http://www.sagemath.org/).
in a format readable by the computer algebra system Sage (http://www.sagemath.org/).  .
.  :
: 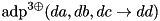 .
.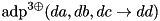 .
.![$A[2][2][2][2] = A[da[i]][db[i]][dc[i]][dd[i]]$](form_141.png) , where
, where![$da[i]$](form_81.png) : the i-th bit of the first input difference.
: the i-th bit of the first input difference.![$db[i]$](form_102.png) : the i-th bit of the second input difference.
: the i-th bit of the second input difference.![$dc[i]$](form_56.png) : the i-th bit of the third input difference.
: the i-th bit of the third input difference.![$dd[i]$](form_142.png) : the i-th bit of the output difference.
: the i-th bit of the output difference. (adp_xor3_sf) into an index.
(adp_xor3_sf) into an index.