 |
YAARX: Yet Another ARX Toolkit
0.1
|
 |
YAARX: Yet Another ARX Toolkit
0.1
|
Automatic search for ADD differential trails in block cipher TEA. More...
#include "common.hh"#include "adp-xor3.hh"#include "tea.hh"#include "eadp-tea-f.hh"#include "tea-f-add-pddt.hh"Functions | |
| uint32_t | tea_add_threshold_count_lp (differential_t trail[NROUNDS], uint32_t trail_len, double p_thres) |
| void | tea_add_threshold_search (const int n, const int nrounds, const uint32_t npairs, const uint32_t key[4], gsl_matrix *A[2][2][2][2], double B[NROUNDS], double *Bn, const differential_t diff_in[NROUNDS], differential_t trail[NROUNDS], uint32_t lsh_const, uint32_t rsh_const, std::multiset< differential_t, struct_comp_diff_p > *diff_mset_p, std::set< differential_t, struct_comp_diff_dx_dy > *diff_set_dx_dy) |
| bool | tea_add_is_trail_in_vector (differential_t trail[NROUNDS], std::vector< std::array< differential_t, NROUNDS >> trail_vec) |
| void | tea_add_threshold_search_full (const int n, const int nrounds, const uint32_t npairs, const uint32_t key[4], gsl_matrix *A[2][2][2][2], double B[NROUNDS], double *Bn, const differential_t diff_in[NROUNDS], differential_t trail[NROUNDS], uint32_t lsh_const, uint32_t rsh_const, std::multiset< differential_t, struct_comp_diff_p > *diff_mset_p, std::set< differential_t, struct_comp_diff_dx_dy > *diff_set_dx_dy, std::multiset< differential_t, struct_comp_diff_p > *croads_diff_mset_p, std::set< differential_t, struct_comp_diff_dx_dy > *croads_diff_set_dx_dy, std::vector< std::array< differential_t, NROUNDS >> *trail_vec) |
| uint32_t | tea_add_trail_search (uint32_t key[4], double B[NROUNDS], differential_t trail[NROUNDS]) |
| uint32_t | tea_add_trail_search_full (uint32_t key[4], double BB[NROUNDS], differential_t trail[NROUNDS], uint32_t num_rounds) |
Automatic search for ADD differential trails in block cipher TEA.
| uint32_t tea_add_threshold_count_lp | ( | differential_t | trail[NROUNDS], |
| uint32_t | trail_len, | ||
| double | p_thres | ||
| ) |
Count the number of differentials in a trail that have probabilities below a given threshold.
| trail | a differential trail for trail_len rounds. |
| trail_len | length of the differential trail. |
| p_thres | probability threshold. |
| void tea_add_threshold_search | ( | const int | n, |
| const int | nrounds, | ||
| const uint32_t | npairs, | ||
| const uint32_t | key[4], | ||
| gsl_matrix * | A[2][2][2][2], | ||
| double | B[NROUNDS], | ||
| double * | Bn, | ||
| const differential_t | diff_in[NROUNDS], | ||
| differential_t | trail[NROUNDS], | ||
| uint32_t | lsh_const, | ||
| uint32_t | rsh_const, | ||
| std::multiset< differential_t, struct_comp_diff_p > * | diff_mset_p, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | diff_set_dx_dy | ||
| ) |
Automatic search for ADD differential trails in block cipher TEA. using pDDT.
| n | index of the current round: 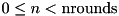 . . |
| nrounds | total number of rounds (NROUNDS). |
| npairs | number of chosen plaintext pairs (NPAIRS). |
| key | cryptographic key of TEA. |
| A | transition probability matrices for 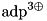 (adp_xor3_sf). (adp_xor3_sf). |
| B | array containing the best differential probabilities for i rounds: 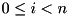 . . |
| Bn | the best probability on 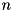 rounds, updated dynamically. rounds, updated dynamically. |
| diff_in | array of differentials. |
| trail | best found differential trail for nrounds. |
| lsh_const | LSH constant (TEA_LSH_CONST). |
| rsh_const | RSH constant (TEA_RSH_CONST). |
| diff_mset_p | set of differentials 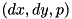 (the pDDT) ordered by probability p. (the pDDT) ordered by probability p. |
| diff_set_dx_dy | set of differentials 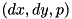 (the pDDT) ordered by index (the pDDT) ordered by index 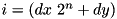 . . |
The outline of the array of bounds 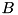 is the following:
is the following:
![$B[0]$](form_325.png) : best probability for
: best probability for 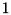 round.
round.![$B[1]$](form_327.png) : best probability for
: best probability for 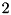 rounds.
rounds.
![$B[i]$](form_329.png) : best probability for
: best probability for 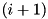 rounds.
rounds.
![$B[n-2]$](form_330.png) : best probability for
: best probability for 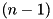 rounds.
rounds.![$B[n-1]$](form_332.png) : best probability for
: best probability for 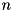 rounds.
rounds.Algorithm Outline:
The algorithm is based on Matsui search strategy described in [Sect. 4, Matsui, On correlation between the order of S-boxes and the strength of DES, EUROCRYPT'94]. The main idea is to view the F-function of TEA as an S-box for which a partial difference distribution table (pDDT) is constructed (tea_f_add_pddt). Then a recursive search for differential trails over a given number of rounds 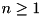 is performed. From knowledge of the best probabilities
is performed. From knowledge of the best probabilities  for the first
for the first 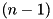 rounds and an initial estimate
rounds and an initial estimate 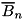 for the probability for
for the probability for 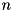 rounds the best probability
rounds the best probability 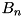 for
for 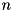 rounds is derived. Note that for the estimate the following must hold:
rounds is derived. Note that for the estimate the following must hold: 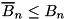 .
.
In addition to Matsui's notation for the probability of the best 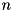 -round trail
-round trail 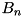 and of its estimation
and of its estimation 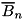 we introduce
we introduce 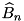 to denote the probability of the best found trail for
to denote the probability of the best found trail for 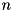 rounds:
rounds: 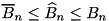 . Given a pDDT
. Given a pDDT 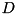 of maximum size
of maximum size 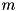 , an estimation for the best
, an estimation for the best 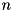 -round probability
-round probability 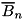 with its corresponding
with its corresponding 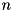 -round differential trail
-round differential trail 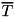 and the probabilities
and the probabilities 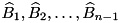 of the best found trails for the first
of the best found trails for the first 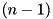 rounds, tea_add_threshold_search outputs an
rounds, tea_add_threshold_search outputs an 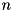 -round trail
-round trail 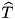 that has probability
that has probability 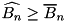 .
.
tea_add_threshold_search operates by recursively extending a trail for 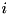 rounds to
rounds to 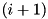 rounds, beginning with
rounds, beginning with 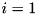 and terminating at
and terminating at 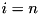 . This is done by exploring multiple differential trails constructed from the entries of the pDDT
. This is done by exploring multiple differential trails constructed from the entries of the pDDT 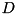 at every round. If, in the process, a differential that is not already in
at every round. If, in the process, a differential that is not already in 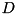 is encountered it is added to
is encountered it is added to 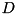 , provided that the maximum size
, provided that the maximum size 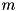 has not been reached. The recursion at level
has not been reached. The recursion at level 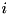 continues to level
continues to level 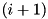 only if the probability of the constructed
only if the probability of the constructed 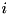 -round trail multiplied by the probability of the best found trail for
-round trail multiplied by the probability of the best found trail for 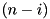 rounds is at least
rounds is at least 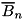 i.e. if,
i.e. if, 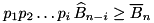 holds. For
holds. For 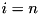 the last equation is equivalent to:
the last equation is equivalent to: 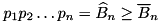 . If the latter holds, the initial estimate is updated with the new:
. If the latter holds, the initial estimate is updated with the new: 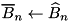 and the corresponding trail is also updated accordingly:
and the corresponding trail is also updated accordingly: 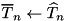 . Upon termination the best found trail
. Upon termination the best found trail 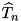 and its probability
and its probability 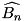 are returned as result.
are returned as result.
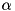 is encountered for which a corresponding output difference
is encountered for which a corresponding output difference 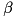 is not found in the pDDT (i.e. the differential
is not found in the pDDT (i.e. the differential 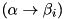 is not in the pDDT for no
is not in the pDDT for no 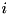 ), then an arbitarary non-zero probability output differnece
), then an arbitarary non-zero probability output differnece 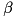 is computed with the nz_eadp_tea_f procedure . See also tea_add_threshold_search_full where a more extensive search over the space of possible output differences
is computed with the nz_eadp_tea_f procedure . See also tea_add_threshold_search_full where a more extensive search over the space of possible output differences 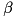 is performed in this case.
is performed in this case.Termination
The algorithm terminates when one of the following two events happens first:
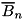 can not be improved further.
can not be improved further.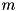 of the pDDT
of the pDDT 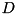 is reached and all differentials in
is reached and all differentials in 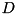 in every round have been explored.
in every round have been explored.Complexity
The complexity of tea_add_threshold_search depends on the following factors:
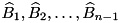 for the first
for the first 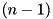 rounds to the actual best probabilities.
rounds to the actual best probabilities.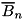 .
.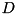 . The latter is determined by the probability threshold used to compute
. The latter is determined by the probability threshold used to compute 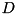 and by the maximum number of elements
and by the maximum number of elements 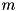 allowed.
allowed.In the worst-case, in every round, except the last, 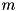 iterations will be executed. Therefore the worst-case complexity is
iterations will be executed. Therefore the worst-case complexity is 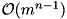 , where
, where 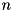 is the number of rounds. Although the algorithm is worst-case exponential in the number of rounds, it is much more efficient in practice.
is the number of rounds. Although the algorithm is worst-case exponential in the number of rounds, it is much more efficient in practice.
npairs pairs of chosen plaintexts.| void tea_add_threshold_search_full | ( | const int | n, |
| const int | nrounds, | ||
| const uint32_t | npairs, | ||
| const uint32_t | key[4], | ||
| gsl_matrix * | A[2][2][2][2], | ||
| double | B[NROUNDS], | ||
| double * | Bn, | ||
| const differential_t | diff_in[NROUNDS], | ||
| differential_t | trail[NROUNDS], | ||
| uint32_t | lsh_const, | ||
| uint32_t | rsh_const, | ||
| std::multiset< differential_t, struct_comp_diff_p > * | diff_mset_p, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | diff_set_dx_dy, | ||
| std::multiset< differential_t, struct_comp_diff_p > * | croads_diff_mset_p, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | croads_diff_set_dx_dy, | ||
| std::vector< std::array< differential_t, NROUNDS >> * | trail_vec | ||
| ) |
Full threshold search for ADD differential trails in block cipher TEA, that uses initial bounds pre-computed with tea_add_threshold_search .
| n | index of the current round: 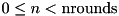 . . |
| nrounds | total number of rounds (NROUNDS). |
| npairs | number of chosen plaintext pairs (NPAIRS). |
| key | cryptographic key of TEA. |
| A | transition probability matrices for 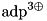 (adp_xor3_sf). (adp_xor3_sf). |
| B | array of initial bounds pre-computed with tea_add_threshold_search . |
| Bn | the best probability on 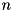 rounds, updated dynamically. rounds, updated dynamically. |
| diff_in | array of differentials. |
| trail | best found differential trail for nrounds. |
| lsh_const | LSH constant (TEA_LSH_CONST). |
| rsh_const | RSH constant (TEA_RSH_CONST). |
| diff_mset_p | set of differentials 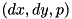 (Highways) ordered by probability p. (Highways) ordered by probability p. |
| diff_set_dx_dy | set of differentials 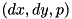 (Highways) ordered by index (Highways) ordered by index 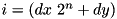 . . |
| croads_diff_mset_p | temporrary set of differentials 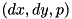 (Countryroads) ordered by probability p. (Countryroads) ordered by probability p. |
| croads_diff_set_dx_dy | set of differentials 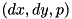 (Countryroads) ordered by index (Countryroads) ordered by index 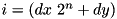 . . |
Algorithm Outline:
The high-level logic of the algorithm is conceptually the same as tea_add_threshold_search . The main difference is in the way it handles the case when an input difference 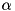 is encountered for which a corresponding output difference
is encountered for which a corresponding output difference 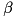 is not found in the pre-computed pDDT. In this case a list of many possible output differences is computed and is explored during the search. More deatiled explanation follows.
is not found in the pre-computed pDDT. In this case a list of many possible output differences is computed and is explored during the search. More deatiled explanation follows.
Let 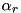 be an input difference to round
be an input difference to round 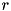 such that the differential
such that the differential 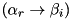 is not in the pDDT for no value of
is not in the pDDT for no value of 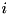 . In this case the algorithm uses tea_f_da_add_pddt to compute all differences
. In this case the algorithm uses tea_f_da_add_pddt to compute all differences 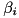 that satisfy the following conditions:
that satisfy the following conditions:
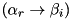 is such that its probability
is such that its probability 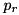 can still improve the probability of the best found trail for the given number of rounds i.e.
can still improve the probability of the best found trail for the given number of rounds i.e. 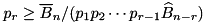 .
.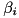 is such that it guarantees that the input difference for the next round
is such that it guarantees that the input difference for the next round 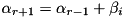 will have a matching entry in the pre-computed pDDT. This condition guarantees that the resulting output difference
will have a matching entry in the pre-computed pDDT. This condition guarantees that the resulting output difference 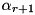 for the next round will have a matching output differences
for the next round will have a matching output differences 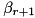 in the initial pDDT.
in the initial pDDT.All differentials 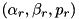 computed according to the above rules are stored in a temporary pDDT. The differentials in this pDDT are explored during the next stages of the search togeter with the differentials from the initial pDDT.
computed according to the above rules are stored in a temporary pDDT. The differentials in this pDDT are explored during the next stages of the search togeter with the differentials from the initial pDDT.
The Highways and Countryroads Analogy
Denote the temporary pDDT constructed as explained above by 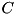 and the initial pDDT that is pre-computed at the start of the search by
and the initial pDDT that is pre-computed at the start of the search by 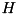 . Then the two tables
. Then the two tables 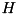 and
and 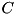 can be thought of as lists of highways and countryroads on a road map. The differentials contained in
can be thought of as lists of highways and countryroads on a road map. The differentials contained in 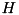 have high probabilities w.r.t. to the fixed probability threshold and correspond therefore to fast roads such as highways. Analogously, the differentials in
have high probabilities w.r.t. to the fixed probability threshold and correspond therefore to fast roads such as highways. Analogously, the differentials in 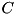 have low probabilities and can be seen as slow roads or countryroads. To continue this analogy, the problem of finding a high probability differential trail for
have low probabilities and can be seen as slow roads or countryroads. To continue this analogy, the problem of finding a high probability differential trail for 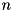 rounds can be seen as a problem of finding a fast route between points
rounds can be seen as a problem of finding a fast route between points 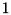 and
and 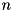 on the map. Clearly such a route must be composed of as many highways as possible. Condition (2), mentioned above, essentially guarantees that any country road that we may take in our search for a fast route will bring us back on a highway. Note that it is possible that the fastest route contains two or more country roads in sequence. While such a case will be missed, it may be accounted for by lowering the initial probability threshold.
on the map. Clearly such a route must be composed of as many highways as possible. Condition (2), mentioned above, essentially guarantees that any country road that we may take in our search for a fast route will bring us back on a highway. Note that it is possible that the fastest route contains two or more country roads in sequence. While such a case will be missed, it may be accounted for by lowering the initial probability threshold.
Full Threshold Search Pseudo-Code

| uint32_t tea_add_trail_search | ( | uint32_t | key[4], |
| double | B[NROUNDS], | ||
| differential_t | trail[NROUNDS] | ||
| ) |
Search for ADD differential trails in block cipher TEA: wrapper function for tea_add_threshold_search.
| key | cryptographic key of TEA. |
| B | array of bounds. |
| trail | best found differential trail. |
Algorithm Outline:
The procedure operates as follows:
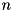 rounds (n = NROUNDS) through a successive application of tea_add_threshold_search :
rounds (n = NROUNDS) through a successive application of tea_add_threshold_search :![$B[0]$](form_325.png) .
.![$B[0]$](form_325.png) compute the best found probability on 2 rounds:
compute the best found probability on 2 rounds: ![$B[1]$](form_327.png) .
.
![$B[0],\ldots,B[i-1]$](form_381.png) compute the best found probability on
compute the best found probability on 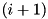 rounds:
rounds: ![$B[i]$](form_329.png) .
.
![$B[0],\ldots,B[n-2]$](form_382.png) compute the best found probability on
compute the best found probability on 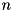 rounds:
rounds: ![$B[n-1]$](form_332.png) .
.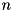 rounds on standrad output and terminate.
rounds on standrad output and terminate.| uint32_t tea_add_trail_search_full | ( | uint32_t | key[4], |
| double | BB[NROUNDS], | ||
| differential_t | trail[NROUNDS], | ||
| uint32_t | num_rounds | ||
| ) |
Full threshold search using bounds pre-computed with tea_add_trail_search ; basically a wrapper function for tea_add_threshold_search_full .
| key | cryptographic key of TEA. |
| BB | array of bounds. |
| trail | best found differential trail. |
The function takes as input an array of initial bounds B and the corresponding best found trail, computed with a prior call to tea_add_trail_search and outputs a trail that is at least as good as the niput.