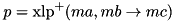YAARX: Yet Another ARX Toolkit  0.1
 All Data Structures Files Functions Variables Macros Pages
Functions
xlp-add.hh File Reference

Header file for xlp-add.cc: More...

Go to the source code of this file.

Functions

double xlp_add_exper (const WORD_T ma, const WORD_T mb, const WORD_T mc, const WORD_T word_size)
 
double xlc_add (const WORD_T ma, const WORD_T mb, const WORD_T mc, const WORD_T word_size)
 
int xlc_add_sign (const WORD_T ma, const WORD_T mb, const WORD_T mc, const WORD_T word_size)
 
double xlp_add (const WORD_T ma, const WORD_T mb, const WORD_T mc, const WORD_T word_size)
 
double xlb_add (const WORD_T ma, const WORD_T mb, const WORD_T mc, const WORD_T word_size)
 
WORD_T get_masks_rev_ibit (const WORD_T ma, const WORD_T mb, const WORD_T mc, const WORD_T word_size, const WORD_T ibit)
 
int xlc_add_log2 (const uint32_t ma, const uint32_t mb, const uint32_t mc, const uint32_t word_size)
 

Detailed Description

Header file for xlp-add.cc:

Author
V.Velichkov, vesse.nosp@m.lin..nosp@m.velic.nosp@m.hkov.nosp@m.@uni..nosp@m.lu
Date
2012-2015

Function Documentation

WORD_T get_masks_rev_ibit ( const WORD_T  ma,
const WORD_T  mb,
const WORD_T  mc,
const WORD_T  word_size,
const WORD_T  ibit 
)
inline

Return the reverse of the ibit-th bit i.e. the bit at position (word_size - ibit - 1)-th of masks ma, mb and mc as an octal word: WORD_T word = (mc_i << 2) | (mb_i << 1) | (ma_i << 0);

double xlb_add ( const WORD_T  ma,
const WORD_T  mb,
const WORD_T  mc,
const WORD_T  word_size 
)

Compute the bias of the following linear approximation of modular addition:

(a . ma) ^ (b . mb) = (c . mc)

where (x . ma) denotes the dot product between the word x and the mask mx.

xlb is computed from xlp using the relation:

xlb = xlp - 1/2

Parameters
mafirst input mask.
mbsecond input mask.
mcoutput mask.
word_sizeword size in bits
Returns
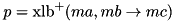
$p = \mathrm{xlb}^{+}(ma, mb \rightarrow mc)$
See Also
xlp_add, xlc_add, xlc_add_sign
double xlc_add ( const WORD_T  ma,
const WORD_T  mb,
const WORD_T  mc,
const WORD_T  word_size 
)
inline

Optimized version of xlc_add_nopt

See Also
xlc_add_nopt

if at state 0 halt (probability = 1/2, bias = 0)

if at state 0 halt (probability = 1/2, bias = 0)

int xlc_add_log2 ( const uint32_t  ma,
const uint32_t  mb,
const uint32_t  mc,
const uint32_t  word_size 
)
inline

The absolute XOR linear correlation of ADD ( 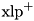$\mathrm{xlp}^{+}$) Complexity: $O(n)$.

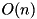XLC is the correlation of the following linear approximation of modular addition, computed over the inputs a and b

(a . ma) ^ (b . mb) = (c . mc)

where (x . ma) denotes the dot product between the word x and the mask mx.

Parameters
mafirst input mask.
mbsecond input mask.
mcoutput mask.
word_sizeword size in bits
Returns
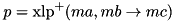
$p = \mathrm{xlp}^{+}(ma, mb \rightarrow mc)$
Note
Relations between linear probability, bias and correlation:

bias = prob - 1/2 corr = (2 * bias) = (2 * prob) - 1

Optimized version

int xlc_add_sign ( const WORD_T  ma,
const WORD_T  mb,
const WORD_T  mc,
const WORD_T  word_size 
)

Compute the sign of the XOR linear correlation of ADD ( 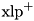$\mathrm{xlp}^{+}$)

Parameters
mafirst input mask.
mbsecond input mask.
mcoutput mask.
word_sizeword size in bits
Returns
sign +1 or -1
See Also
xlc_add
double xlp_add ( const WORD_T  ma,
const WORD_T  mb,
const WORD_T  mc,
const WORD_T  word_size 
)

The XOR linear probability of ADD ( 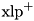$\mathrm{xlp}^{+}$) Complexity: $O(n)$.

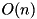XLP is the probability over the inputs a and b that the following equation holds:

(a . ma) ^ (b . mb) = (c . mc)

where (x . ma) denotes the dot product between the word x and the mask mx.

xlp is computed from xlc using the relation:

xlc = (2 * xlp) - 1

together with the fact that the sign of xlc is -1 iff HW((ma ^ mc) & (mb ^ mc)) is odd.

Parameters
mafirst input mask.
mbsecond input mask.
mcoutput mask.
word_sizeword size in bits
Returns
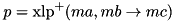
$p = \mathrm{xlp}^{+}(ma, mb \rightarrow mc)$
See Also
xlc_add, xlc_add_sign
double xlp_add_exper ( const WORD_T  ma,
const WORD_T  mb,
const WORD_T  mc,
const WORD_T  word_size 
)

The XOR linear probability of ADD ( 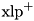$\mathrm{xlp}^{+}$) computed experimentally over all inputs. Complexity: $O(2^{2n})$.

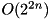XLP is the probability over the inputs a and b that the following equation holds:

(a . ma) ^ (b . mb) = (c . mc)

where (x . ma) denotes the dot product between the word x and the mask mx.

Parameters
mafirst input mask.
mbsecond input mask.
mcoutput mask.
word_sizeword size in bits
Returns
$p = \mathrm{xlp}^{+}(ma, mb \rightarrow mc)$
See Also
xlp_add