YAARX: Yet Another ARX Toolkit  0.1
 All Data Structures Files Functions Variables Macros Pages
Functions
xdp-xtea-f-fk.hh File Reference

Header file for xdp-xtea-f-fk.cc. More...

Go to the source code of this file.

Functions

double xdp_xtea_f_fk_exper (const uint32_t da, const uint32_t db, const uint32_t k, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const)
 
double xdp_xtea_f_fk_approx (const uint32_t ninputs, const uint32_t da, const uint32_t db, const uint32_t k, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const)
 
bool xdp_xtea_f_check_x (const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t k, const uint32_t delta, const uint32_t dx, const uint32_t dy, const uint32_t x)
 
bool xdp_xtea_f_is_sat (const uint32_t mask_i, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t k, const uint32_t delta, const uint32_t dx, const uint32_t dy, const uint32_t x)
 
uint32_t xdp_xtea_f_assign_bit_x (const uint32_t n, const uint32_t i, const uint32_t mask_i, const uint32_t x, const uint32_t key, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t dx, const uint32_t dy, uint32_t *x_cnt, double *prob)
 
double xdp_xtea_f_fk (const uint32_t n, const uint32_t dx, const uint32_t dy, const uint32_t key, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const)
 
double xdp_xtea_f2_fk_exper (const uint32_t daa, const uint32_t da, const uint32_t db, const uint32_t k, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const)
 
double xdp_xtea_f2_fk_approx (const uint32_t ninputs, const uint32_t daa, const uint32_t da, const uint32_t db, const uint32_t k, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const)
 
bool xdp_xtea_f2_check_x_xx (const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t k, const uint32_t delta, const uint32_t dxx, const uint32_t dx, const uint32_t dy, const uint32_t xx, const uint32_t x)
 
bool xdp_xtea_f2_is_sat (const uint32_t mask_i, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t k, const uint32_t delta, const uint32_t dxx, const uint32_t dx, const uint32_t dy, const uint32_t xx, const uint32_t x)
 
uint32_t xdp_xtea_f2_assign_bit_x_xx (const uint32_t n, const uint32_t i, const uint32_t mask_i, const uint32_t xx, const uint32_t x, const uint32_t key, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t dxx, const uint32_t dx, const uint32_t dy, uint64_t *x_cnt, double *prob)
 
double xdp_xtea_f2_fk (const uint32_t n, const uint32_t dxx, const uint32_t dx, const uint32_t dy, const uint32_t key, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const)
 
double nz_xdp_xtea_f (gsl_matrix *A[2][2][2], const uint32_t dx, uint32_t *dy, uint32_t lsh_const, uint32_t rsh_const)
 

Detailed Description

Header file for xdp-xtea-f-fk.cc.

Author
V.Velichkov, vesse.nosp@m.lin..nosp@m.velic.nosp@m.hkov.nosp@m.@uni..nosp@m.lu
Date
2012-2013

Function Documentation

double nz_xdp_xtea_f ( gsl_matrix *  A[2][2][2],
const uint32_t  dx,
uint32_t *  dy,
uint32_t  lsh_const,
uint32_t  rsh_const 
)

For the XTEA F-function (xtea_f), for fixed input difference dx, compute an output difference dy such that the differential $(dx \rightarrow dy)$ has non-zero probability.

Parameters
Atransition probability matrices for $\mathrm{xdp}^{+}$ (xdp_add_sf).
dxinput difference.
dyoutput difference.
lsh_constLSH constant.
rsh_constRSH constant.
Returns
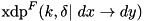
$\mathrm{xdp}^{F}(k, \delta |~ dx \rightarrow dy)$

Algorithm sketch:

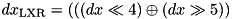  1. Compute the output XOR difference after xtea_f_lxr : $dx_{\mathrm{LXR}} = (((dx \ll 4) \oplus (dx \gg 5))$.
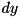  2. Compute the maximum probability output difference $dy$ after the modular addition of xtea_f : 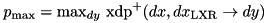$p_{\mathrm{max}} = \mathrm{max}_{dy}~\mathrm{xdp}^{+}(dx, dx_\mathrm{LXR} \rightarrow dy)$ (see max_xdp_add).
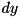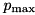  3. Store $dy$ and return $p_{\mathrm{max}}$.
Attention
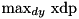In the computation of $\mathrm{max}_{dy}~\mathrm{xdp}$ the inputs to the addition are implicitly assumed to be independent. Clearly they are not and so the returned probability is only an approximation.
uint32_t xdp_xtea_f2_assign_bit_x_xx ( const uint32_t  n,
const uint32_t  i,
const uint32_t  mask_i,
const uint32_t  xx,
const uint32_t  x,
const uint32_t  key,
const uint32_t  delta,
const uint32_t  lsh_const,
const uint32_t  rsh_const,
const uint32_t  dxx,
const uint32_t  dx,
const uint32_t  dy,
uint64_t *  x_cnt,
double *  prob 
)

Counts the number of values xx and x for which the XOR differential 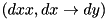$(dxx, dx \rightarrow dy)$ of the XTEA F-function with two inputs 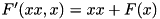$F'(xx, x) = xx + F(x)$ (see xtea_f2) is satisfied. The algorithm operates by recursively assigning the bits of xx and x starting from bit position i and terminating at the MS bit n. The recursion proceeds to bit 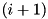$(i+1)$ only if the differential is satisfied on the i LS bits. This is checked by applying xdp_xtea_f2_is_sat.

Parameters
nword size (terminating bit popsition).
icurrent bit position.
mask_imask on the i LS bits of x.
xxfirst input value.
xsecond input value of size at least (i + rsh_const).
keyround key.
deltaround constant.
lsh_constLSH constant.
rsh_constRSH constant.
dxxfirst input difference.
dxsecond input difference.
dyoutput difference.
x_cntnumber of values satisfying $(dx \rightarrow dy)$.
probthe fixed-key XOR probability of F': 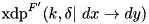$\mathrm{xdp}^{F'}(k, \delta |~ dx \rightarrow dy)$.
Returns
1 if $x[i-1:0]$ satisfies $(dx[i-1:0] \rightarrow dy[i-1:0])$; 0 otherwise.
See Also
xdp_xtea_f2_fk
Note
x_cnt counts both the values for x and for xx.
bool xdp_xtea_f2_check_x_xx ( const uint32_t  lsh_const,
const uint32_t  rsh_const,
const uint32_t  k,
const uint32_t  delta,
const uint32_t  dxx,
const uint32_t  dx,
const uint32_t  dy,
const uint32_t  xx,
const uint32_t  x 
)

Check if given input values xx and x satisfy the XOR differential 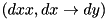$(dxx, dx \rightarrow dy)$ of the XTEA F-function with two inputs 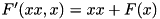$F'(xx, x) = xx + F(x)$ (see xtea_f2).

Parameters
lsh_constLSH constant.
rsh_constRSH constant.
kround key.
deltaround constant.
dxxfirst input difference.
dxsecond input difference.
dyoutput difference.
xxfirst input value.
xsecond input value.
Returns
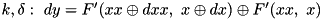TRUE if $k, \delta:~ dy = F'(xx \oplus dxx,~ x \oplus dx) \oplus F'(xx,~ x)$.
double xdp_xtea_f2_fk ( const uint32_t  n,
const uint32_t  dxx,
const uint32_t  dx,
const uint32_t  dy,
const uint32_t  key,
const uint32_t  delta,
const uint32_t  lsh_const,
const uint32_t  rsh_const 
)

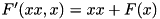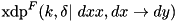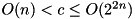Compute the fixed-key, fixed-constant XOR differential probability of of the XTEA F-function with two inputs $F'(xx, x) = xx + F(x)$ (see xtea_f2): $\mathrm{xdp}^{F}(k, \delta |~ dxx, dx \rightarrow dy)$. Complexity: $ O(n) < c \le O(2^{2n}) $.

Parameters
nword size.
dxxfirst input difference.
dxsecond input difference.
dyoutput difference.
keyround key.
deltaround constant.
lsh_constLSH constant.
rsh_constRSH constant.
Returns
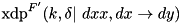$\mathrm{xdp}^{F'}(k, \delta |~ dxx, dx \rightarrow dy)$.
See Also
xdp_xtea_f2_assign_bit_x_xx
double xdp_xtea_f2_fk_approx ( const uint32_t  ninputs,
const uint32_t  daa,
const uint32_t  da,
const uint32_t  db,
const uint32_t  k,
const uint32_t  delta,
const uint32_t  lsh_const,
const uint32_t  rsh_const 
)

An approximation of the XDP of the XTEA F-function with two inputs 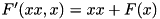$F'(xx, x) = xx + F(x)$ (see xtea_f2), obtained over a number of input chosen plaintext pairs c hosen uniformly at random.

Parameters
ninputsnumber of input chosen plaintext pairs.
daafirst input difference.
dasecond input difference.
dboutput difference.
kround key.
deltaround constant.
lsh_constLSH constant.
rsh_constRSH constant.
Returns
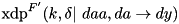$\mathrm{xdp}^{F'}(k, \delta |~ daa, da \rightarrow dy)$.
double xdp_xtea_f2_fk_exper ( const uint32_t  daa,
const uint32_t  da,
const uint32_t  db,
const uint32_t  k,
const uint32_t  delta,
const uint32_t  lsh_const,
const uint32_t  rsh_const 
)

Compute the fixed-key through exhaustive search over all input values the fixed-constant XOR differential probability of the F-function of block cipher XTEA including the second modular addition and denoted by 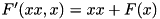$F'(xx, x) = xx + F(x)$ (see xtea_f2): 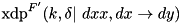$\mathrm{xdp}^{F'}(k, \delta |~ dxx, dx \rightarrow dy)$. Complexity: $O(2^{2n})$.

Parameters
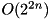daafirst input difference.
dasecond input difference.
dboutput difference.
kround key.
deltaround constant.
lsh_constLSH constant.
rsh_constRSH constant.
Returns
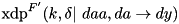$\mathrm{xdp}^{F'}(k, \delta |~ daa, da \rightarrow dy)$.
bool xdp_xtea_f2_is_sat ( const uint32_t  mask_i,
const uint32_t  lsh_const,
const uint32_t  rsh_const,
const uint32_t  k,
const uint32_t  delta,
const uint32_t  dxx,
const uint32_t  dx,
const uint32_t  dy,
const uint32_t  xx,
const uint32_t  x 
)

Check if the XOR differential 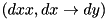$(dxx, dx \rightarrow dy)$ of the XTEA F-function with two inputs 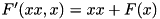$F'(xx, x) = xx + F(x)$ (see xtea_f2) is satisfied on the i LS bits of xx and x i.e. check if

\[k, \delta:~ dy[i-1:0] = F(xx[i-1:0], x[i-1:0] \oplus dx[i-1:0]) \oplus F(xx[i-1:0], x[i-1:0])\]

Parameters
mask_ii bit mask.
lsh_constLSH constant.
rsh_constRSH constant.
kround key.
deltaround constant.
dxxfirst input difference.
dxsecond input difference.
dyoutput difference.
xxfirst input value.
xsecond input value of size at least (i + rsh_const).
Returns
TRUE if the differential is satisfied; FALSE otherwise.
Attention
x must be of size at least 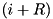$(i + R)$ bits where R is the RSH constant of F.
uint32_t xdp_xtea_f_assign_bit_x ( const uint32_t  n,
const uint32_t  i,
const uint32_t  mask_i,
const uint32_t  x,
const uint32_t  key,
const uint32_t  delta,
const uint32_t  lsh_const,
const uint32_t  rsh_const,
const uint32_t  dx,
const uint32_t  dy,
uint32_t *  x_cnt,
double *  prob 
)

Counts the number of values x for which the differential $(dx \rightarrow dy)$ for the F-function of XTEA is satisfied. The function operates by recursively assigning the bits of x starting from bit position i and terminating at the MS bit n. The recursion proceeds to bit 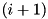$(i+1)$ only if the differential is satisfied on the i LS bits. This is checked by applying xdp_xtea_f_is_sat.

Parameters
nword size (terminating bit popsition).
icurrent bit position.
mask_imask on the i LS bits of x.
xinput value of size at least (i + rsh_const).
keyround key.
deltaround constant.
lsh_constLSH constant.
rsh_constRSH constant.
dxinput difference.
dyoutput difference.
x_cntnumber of values satisfying $(dx \rightarrow dy)$.
probthe fixed-key XOR probability of F: 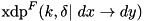$\mathrm{xdp}^{F}(k, \delta |~ dx \rightarrow dy)$.
Returns
1 if $x[i-1:0]$ satisfies $(dx[i-1:0] \rightarrow dy[i-1:0])$; 0 otherwise.
See Also
xdp_xtea_f_fk
bool xdp_xtea_f_check_x ( const uint32_t  lsh_const,
const uint32_t  rsh_const,
const uint32_t  k,
const uint32_t  delta,
const uint32_t  dx,
const uint32_t  dy,
const uint32_t  x 
)

Check if a given value x satisfies the XOR differential $(dx \rightarrow dy)$ for the XTEA F-function.

Parameters
lsh_constLSH constant.
rsh_constRSH constant.
kround key.
deltaround constant.
dxinput difference.
dyoutput difference.
xinput value.
Returns
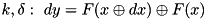TRUE if $k, \delta:~ dy = F(x \oplus dx) \oplus F(x)$.
double xdp_xtea_f_fk ( const uint32_t  n,
const uint32_t  dx,
const uint32_t  dy,
const uint32_t  key,
const uint32_t  delta,
const uint32_t  lsh_const,
const uint32_t  rsh_const 
)

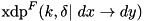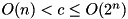Compute the fixed-key, fixed-constant XOR differential probability of the F-function of block cipher XTEA: $\mathrm{xdp}^{F}(k, \delta |~ dx \rightarrow dy)$. Complexity: $ O(n) < c \le O(2^n) $.

Parameters
nword size.
dxinput difference.
dyoutput difference.
keyround key.
deltaround constant.
lsh_constLSH constant.
rsh_constRSH constant.
Returns
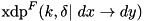$\mathrm{xdp}^{F}(k, \delta |~ dx \rightarrow dy)$.
See Also
xdp_xtea_f_assign_bit_x
double xdp_xtea_f_fk_approx ( const uint32_t  ninputs,
const uint32_t  da,
const uint32_t  db,
const uint32_t  k,
const uint32_t  delta,
const uint32_t  lsh_const,
const uint32_t  rsh_const 
)

An approximation of the XDP of the XTEA F-function (xtea_f) obtained over a number of input chosen plaintext pairs chosen uniformly at random.

Parameters
ninputsnumber of input chosen plaintext pairs.
dainput difference.
dboutput difference.
kround key.
deltaround constant.
lsh_constLSH constant.
rsh_constRSH constant.
Returns
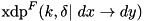$\mathrm{xdp}^{F}(k, \delta |~ dx \rightarrow dy)$.
double xdp_xtea_f_fk_exper ( const uint32_t  da,
const uint32_t  db,
const uint32_t  k,
const uint32_t  delta,
const uint32_t  lsh_const,
const uint32_t  rsh_const 
)

Compute the fixed-key, fixed-constant XOR differential probability of the F-function of block cipher XTEA: 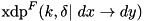$\mathrm{xdp}^{F}(k, \delta |~ dx \rightarrow dy)$ through exhaustive search over all input values. Complexity: $O(2^n)$.

Parameters
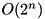dainput difference.
dboutput difference.
kround key.
deltaround constant.
lsh_constLSH constant.
rsh_constRSH constant.
Returns
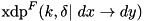$\mathrm{xdp}^{F}(k, \delta |~ dx \rightarrow dy)$.
bool xdp_xtea_f_is_sat ( const uint32_t  mask_i,
const uint32_t  lsh_const,
const uint32_t  rsh_const,
const uint32_t  k,
const uint32_t  delta,
const uint32_t  dx,
const uint32_t  dy,
const uint32_t  x 
)

Check if the differential $(dx \rightarrow dy)$ for F (xtea_f) is satisfied on the i LS bits of x i.e. check if

$k, \delta:~ dy[i-1:0] = F(x[i-1:0] \oplus dx[i-1:0]) \oplus F(x[i-1:0])$.

Attention
x must be of size at least 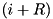$(i + R)$ bits where R is the RSH constant of F.
Parameters
mask_ii bit mask.
lsh_constLSH constant.
rsh_constRSH constant.
kround key.
deltaround constant.
dxinput difference.
dyoutput difference.
xinput value of size at least (i + rsh_const).
Returns
TRUE if $k, \delta:~ dy[i-1:0] = F(x[i-1:0] \oplus dx[i-1:0]) \oplus F(x[i-1:0])$.