Header file for xdp-add.cc:
More...
Go to the source code of this file.
|
| void | xdp_add_alloc_matrices (gsl_matrix *A[2][2][2]) |
| |
| void | xdp_add_free_matrices (gsl_matrix *A[2][2][2]) |
| |
| void | xdp_add_normalize_matrices (gsl_matrix *A[2][2][2]) |
| |
| void | xdp_add_print_matrices (gsl_matrix *A[2][2][2]) |
| |
| void | xdp_add_print_matrices_sage (gsl_matrix *A[2][2][2]) |
| |
| void | xdp_add_sf (gsl_matrix *A[2][2][2]) |
| |
| double | xdp_add (gsl_matrix *A[2][2][2], WORD_T da, WORD_T db, WORD_T dc) |
| |
| double | xdp_add_exper (const WORD_T da, const WORD_T db, const WORD_T dc) |
| |
| WORD_T | aop (WORD_T x, WORD_T n_in) |
| |
| WORD_T | cap (WORD_T x, WORD_T y) |
| |
| bool | is_eq (WORD_T x, WORD_T y, WORD_T z) |
| |
| WORD_T | eq (const WORD_T x, const WORD_T y, const WORD_T z) |
| |
|
WORD_T | eq (const WORD_T x, const WORD_T y, const WORD_T z, const uint32_t word_size) |
| |
| bool | xdp_add_is_nonzero (WORD_T da, WORD_T db, WORD_T dc) |
| |
| double | xdp_add_lm (WORD_T da, WORD_T db, WORD_T dc) |
| |
| double | xdp_add_lm (WORD_T da, WORD_T db, WORD_T dc, uint32_t word_size) |
| |
| int | xdp_add_lm_log2 (WORD_T da, WORD_T db, WORD_T dc) |
| |
| int | xdp_add_lm_log2 (WORD_T da, WORD_T db, WORD_T dc, uint32_t word_size) |
| |
Sum of non-zero elements in one column of the  matrices.
matrices.
Initial state for computing the  S-function.
S-function.
Number of state values in the  S-function.
S-function.
| #define XDP_ADD_NINPUTS 2 |
Number of inputs to the XOR operation.
| #define XDP_ADD_NMATRIX 8 |
Number of  matrices.
matrices.
Normalization factor for the  matrices.
matrices.
| WORD_T aop |
( |
WORD_T |
x, |
|
|
WORD_T |
n_in |
|
) |
| |
The all-one parity function (AOP) [Algorithm 1, Lipmaa, Moriai, FSE 2001]
y = aop(x): y[i] = 1 iff x[i..j] = 11..1 has odd length .
| WORD_T cap |
( |
WORD_T |
x, |
|
|
WORD_T |
y |
|
) |
| |
| WORD_T eq |
( |
const WORD_T |
x, |
|
|
const WORD_T |
y, |
|
|
const WORD_T |
z |
|
) |
| |
| bool is_eq |
( |
WORD_T |
x, |
|
|
WORD_T |
y, |
|
|
WORD_T |
z |
|
) |
| |
Check if three integers are equal.
- Parameters
-
| x | first input word |
| y | second input word. |
| z | third input word. |
- Returns
TRUE if 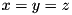 ;
; FALSE otherwise.
| double xdp_add |
( |
gsl_matrix * |
A[2][2][2], |
|
|
WORD_T |
da, |
|
|
WORD_T |
db, |
|
|
WORD_T |
dc |
|
) |
| |
| void xdp_add_alloc_matrices |
( |
gsl_matrix * |
A[2][2][2] | ) |
|
Allocate memory for the transition probability matrices for  .
.
- Parameters
-
| A | transition probability matrices for  . . |
- See Also
- xdp_add_free_matrices
| double xdp_add_exper |
( |
const WORD_T |
da, |
|
|
const WORD_T |
db, |
|
|
const WORD_T |
dc |
|
) |
| |
| void xdp_add_free_matrices |
( |
gsl_matrix * |
A[2][2][2] | ) |
|
Free memory reserved by a previous call to xdp_add_alloc_matrices.
- Parameters
-
| A | transition probability matrices for  . . |
| bool xdp_add_is_nonzero |
( |
WORD_T |
da, |
|
|
WORD_T |
db, |
|
|
WORD_T |
dc |
|
) |
| |
Checks of the differential (da, db -> dc) is possible.
| double xdp_add_lm |
( |
WORD_T |
da, |
|
|
WORD_T |
db, |
|
|
WORD_T |
dc |
|
) |
| |
|
inline |
The XOR differential probability of ADD (  ), as proposed in [Algorithm 2, Lipmaa, Moriai, FSE 2001]. Complexity:
), as proposed in [Algorithm 2, Lipmaa, Moriai, FSE 2001]. Complexity: 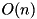 .
.
- Parameters
-
| da | first input difference. |
| db | second input difference. |
| dc | output difference. |
- Returns
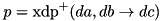
- See Also
- xdp_add
Credits: Yann Le Corre for optimizations
| double xdp_add_lm |
( |
WORD_T |
da, |
|
|
WORD_T |
db, |
|
|
WORD_T |
dc, |
|
|
uint32_t |
word_size |
|
) |
| |
|
inline |
Same as xdp_add_lm but taking the word size as an input parameter – used to compute the prob. of partial differentials
Credits: Yann Le Corre for optimizations
| int xdp_add_lm_log2 |
( |
WORD_T |
da, |
|
|
WORD_T |
db, |
|
|
WORD_T |
dc |
|
) |
| |
|
inline |
The log base 2 of the XOR differential probability of ADD (  ), as proposed in [Algorithm 2, Lipmaa, Moriai, FSE 2001]. Complexity:
), as proposed in [Algorithm 2, Lipmaa, Moriai, FSE 2001]. Complexity: 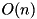 .
.
- Parameters
-
| da | first input difference. |
| db | second input difference. |
| dc | output difference. |
- Returns
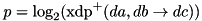
- See Also
- xdp_add_lm
Credits: Yann Le Corre
| int xdp_add_lm_log2 |
( |
WORD_T |
da, |
|
|
WORD_T |
db, |
|
|
WORD_T |
dc, |
|
|
uint32_t |
word_size |
|
) |
| |
|
inline |
| void xdp_add_normalize_matrices |
( |
gsl_matrix * |
A[2][2][2] | ) |
|
Transform the elements of A into probabilities.
- Parameters
-
| A | transition probability matrices for  . . |
| void xdp_add_print_matrices |
( |
gsl_matrix * |
A[2][2][2] | ) |
|
Print the matrices for  .
.
- Parameters
-
| A | transition probability matrices for  . . |
| void xdp_add_print_matrices_sage |
( |
gsl_matrix * |
A[2][2][2] | ) |
|
Print the matrices for  in a format readable by the computer algebra system Sage (http://www.sagemath.org/).
in a format readable by the computer algebra system Sage (http://www.sagemath.org/).
- Parameters
-
| A | transition probability matrices for  . . |
| void xdp_add_sf |
( |
gsl_matrix * |
A[2][2][2] | ) |
|


 matrices.
matrices.  S-function.
S-function.  S-function.
S-function.  matrices.
matrices.  matrices.
matrices. 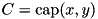 .
.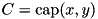 :
:![$C[i] = 1$](form_458.png) if
if ![$L[i]$](form_459.png) is even and non-zero,
is even and non-zero, 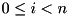 .
.![$C[i] = 0$](form_460.png) if
if ![$L[i]$](form_459.png) is odd.
is odd.![$C[i] = ?$](form_461.png) if
if ![$L[i] = 0$](form_462.png) (
( 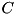 is unspecified).
is unspecified).![$L[i]$](form_459.png) is the length of the longest common alternating chain:
is the length of the longest common alternating chain: ![$(x[i] = y[i]) \neq (x[i+1] = y[i+1]) \neq ... \neq (x[i + L[i]] = y[i + L[i]])$](form_463.png) .
.![$(x[i] = y[i]) \wedge (x[i+1] \neq y[i+1])$](form_464.png) then
then ![$L[i] = 1$](form_465.png) and
and ![$C[i] = 0$](form_460.png) .
.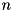 -bit input words
-bit input words 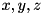 compute an
compute an 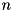 -bit output word
-bit output word 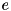 such that
such that ![$e[i] = 1 \iff x[i] = y[i] = z[i]$](form_468.png) and
and ![$e[i] = 0$](form_469.png) otherwise;
otherwise; 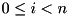 .
.![$e : e[i] = 1 \iff x[i] = y[i] = z[i],~ 0 \le i < n$](form_470.png) .
.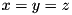 ;
;  ). Complexity:
). Complexity: 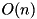 .
. computed with xdp_add_sf.
computed with xdp_add_sf. 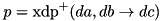
 .
.  .
.  ) computed experimentally over all inputs. Complexity:
) computed experimentally over all inputs. Complexity: 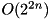 .
.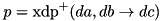
 .
.  ), as proposed in [Algorithm 2, Lipmaa, Moriai, FSE 2001]. Complexity:
), as proposed in [Algorithm 2, Lipmaa, Moriai, FSE 2001]. Complexity: 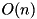 .
.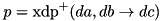
 ), as proposed in [Algorithm 2, Lipmaa, Moriai, FSE 2001]. Complexity:
), as proposed in [Algorithm 2, Lipmaa, Moriai, FSE 2001]. Complexity: 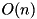 .
.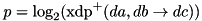
 .
.  .
.  .
.  in a format readable by the computer algebra system Sage (http://www.sagemath.org/).
in a format readable by the computer algebra system Sage (http://www.sagemath.org/). .
.  :
: 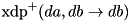 .
.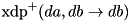 .
.![$A[2][2][2] = A[da[i]][db[i]][dc[i]]$](form_137.png) , where
, where![$da[i]$](form_81.png) : the i-th bit of the first input difference.
: the i-th bit of the first input difference.![$db[i]$](form_102.png) : the i-th bit of the second input difference.
: the i-th bit of the second input difference.![$dc[i]$](form_56.png) : the i-th bit of the output difference.
: the i-th bit of the output difference.