The maximum XOR differential probability of ADD: 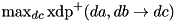 .
More...
.
More...
#include "common.hh"
#include "xdp-add.hh"
|
| void | max_xdp_add_i (const int i, const uint32_t k, const uint32_t n, double *p, WORD_T *dd, gsl_matrix *A[2][2][2], gsl_vector *B[WORD_SIZE+1], gsl_vector *C, const WORD_T da, const WORD_T db, WORD_T *dd_max, double *p_max, uint32_t A_size) |
| |
| void | max_xdp_add_bounds (gsl_matrix *A[2][2][2], gsl_vector *B[WORD_SIZE+1], const WORD_T da, const WORD_T db, WORD_T *dd_max, uint32_t A_size) |
| |
| double | max_xdp_add (gsl_matrix *A[2][2][2], const WORD_T da, const WORD_T db, WORD_T *dd_max) |
| |
| double | max_xdp_add_exper (gsl_matrix *A[2][2][2], const WORD_T da, const WORD_T db, WORD_T *dc_max) |
| |
| double | max_xdp_add_lm (WORD_T da, WORD_T db, WORD_T *dc_ret) |
| |
The maximum XOR differential probability of ADD: 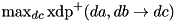 .
.
- Author
- V.Velichkov, vesse.nosp@m.lin..nosp@m.velic.nosp@m.hkov.nosp@m.@uni..nosp@m.lu
| double max_xdp_add |
( |
gsl_matrix * |
A[2][2][2], |
|
|
const WORD_T |
da, |
|
|
const WORD_T |
db, |
|
|
WORD_T * |
dd_max |
|
) |
| |
| void max_xdp_add_bounds |
( |
gsl_matrix * |
A[2][2][2], |
|
|
gsl_vector * |
B[WORD_SIZE+1], |
|
|
const WORD_T |
da, |
|
|
const WORD_T |
db, |
|
|
WORD_T * |
dd_max, |
|
|
uint32_t |
A_size |
|
) |
| |
Compute an array of bounds that can be used in the computation of the maximum differential probability.
- Parameters
-
| A | transition probability matrices. |
| B | array of size A_size rows by (n + 1) columns containing upper bounds on the maximum probabilities of all j bit differentials 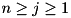 beginning from any state beginning from any state i: A_size 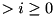 . . |
| da | first input difference. |
| db | second input difference. |
| dd_max | maximum probability output difference. |
| A_size | size of the square transition probability matrices (equivalently, the number of states of the S-function). |
- See Also
- max_xdp_add_i, max_adp_xor_bounds
| double max_xdp_add_exper |
( |
gsl_matrix * |
A[2][2][2], |
|
|
const WORD_T |
da, |
|
|
const WORD_T |
db, |
|
|
WORD_T * |
dc_max |
|
) |
| |
Compute the maximum differential probability by exhaustive search over all output differences. Complexity: 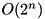 .
.
- Parameters
-
| A | transition probability matrices. |
| da | first input difference. |
| db | second input difference. |
| dc_max | maximum probability output difference. |
- Returns
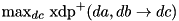 .
.
- See Also
- max_xdp_add
| void max_xdp_add_i |
( |
const int |
i, |
|
|
const uint32_t |
k, |
|
|
const uint32_t |
n, |
|
|
double * |
p, |
|
|
WORD_T * |
dd, |
|
|
gsl_matrix * |
A[2][2][2], |
|
|
gsl_vector * |
B[WORD_SIZE+1], |
|
|
gsl_vector * |
C, |
|
|
const WORD_T |
da, |
|
|
const WORD_T |
db, |
|
|
WORD_T * |
dd_max, |
|
|
double * |
p_max, |
|
|
uint32_t |
A_size |
|
) |
| |
| double max_xdp_add_lm |
( |
WORD_T |
da, |
|
|
WORD_T |
db, |
|
|
WORD_T * |
dc_ret |
|
) |
| |


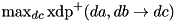 .
More...
.
More...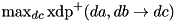 .
. 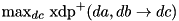 . Complexity c:
. Complexity c: 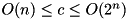 .
.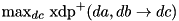 .
.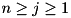 beginning from any state
beginning from any state 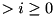 .
. 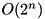 .
.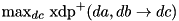 .
.![$B[k][i]$](form_242.png) on the maximum probability of the differential
on the maximum probability of the differential ![$(da[n-1:k], db[n-1:k] \rightarrow dc[n-1:k])$](form_243.png) starting from initial state
starting from initial state ![$\mathrm{dp}(da[n-1:k],db[n-1:k] \rightarrow dc[n-1:k]) = L A_{n-1} A_{n-2} \ldots A_{k} C^{i}_{k-1}$](form_244.png) , given the upper bounds
, given the upper bounds ![$B[k][i]$](form_242.png) on the probabilities of the differentials
on the probabilities of the differentials ![$(da[n-1:j], db[n-1:j] \rightarrow dc[n-1:j])$](form_245.png) for
for 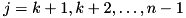 , where
, where ![$L = [1~1~\ldots~1]$](form_246.png) is a row vector of size
is a row vector of size 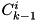 is a unit column vector of size
is a unit column vector of size 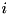 and
and 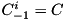 .
.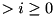 .
. 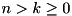 .
. 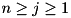 beginning from any state
beginning from any state 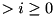 .
. 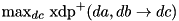 . Complexity c:
. Complexity c: 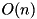 .
.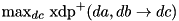 .
.