Header file for max-adp-xor.cc. More...

Functions
void	max_adp_xor_i (const WORD_T i, const WORD_T k, const WORD_T n, double p, WORD_T dd, gsl_matrix A[2][2][2], gsl_vector B[WORD_SIZE+1], gsl_vector C, const WORD_T da, const WORD_T db, WORD_T dd_max, double *p_max, WORD_T A_size)

void	max_adp_xor_bounds (gsl_matrix A[2][2][2], gsl_vector B[WORD_SIZE+1], const WORD_T da, const WORD_T db, WORD_T *dd_max, WORD_T A_size)

double	max_adp_xor (gsl_matrix A[2][2][2], const WORD_T da, const WORD_T db, WORD_T dd_max)

double	max_adp_xor_exper (gsl_matrix A[2][2][2], const WORD_T da, const WORD_T db, WORD_T dc_max)

Detailed Description

Header file for max-adp-xor.cc.

Author: V.Velichkov, vesse.nosp@m.lin..nosp@m.velic.nosp@m.hkov.nosp@m.@uni..nosp@m.lu

Date: 2012-2013

Function Documentation

double max_adp_xor	(	gsl_matrix *	A[2][2][2],
		const WORD_T	da,
		const WORD_T	db,
		WORD_T *	dd_max
	)

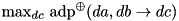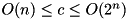Compute the maximum differential probability over all output differences: $\mathrm{max}_{dc}~\mathrm{adp}^{\oplus}(da,db \rightarrow dc)$ . Complexity c: $O(n) \le c \le O(2^n)$ .

Parameters

A	transition probability matrices.
da	first input difference.
db	second input difference.
dd_max	maximum probability output difference.

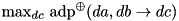Returns: $\mathrm{max}_{dc}~\mathrm{adp}^{\oplus}(da,db \rightarrow dc)$ .

See Also: max_adp_xor_bounds, max_adp_xor_i

void max_adp_xor_bounds	(	gsl_matrix *	A[2][2][2],
		gsl_vector *	B[WORD_SIZE+1],
		const WORD_T	da,
		const WORD_T	db,
		WORD_T *	dd_max,
		WORD_T	A_size
	)

Compute an array of bounds that can be used in the computation of the maximum differential probability.

Parameters

A	transition probability matrices.
B	array of size `A_size` rows by (`n` + 1) columns containing upper bounds on the maximum probabilities of all `j` bit differentials 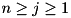$n \ge j \ge 1$ beginning from any state `i:` `A_size` $> i \ge 0$ .
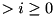da	first input difference.
db	second input difference.
dd_max	maximum probability output difference.
A_size	size of the square transition probability matrices (equivalently, the number of states of the S-function).

Algorithm Outline:

Initialize $B[n][i] \leftarrow 1,~\forall i:~0 \le i < (A_{\mathrm{size}} - 1)$
For every bit position k from n-1 down to 0
- For every state i from 0 to (A_size - 1)
  - Initialize $B[k][i] \leftarrow p_{\mathrm{max}} = 0$
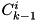  - Let $C^{i}_{k-1}$ be a column unit vector of size A_size with 1 at position i
  - Recursively assign values to the bits of the output difference dc starting at bit popsition 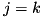and terminating at bit position n.
    - The recursion proceeds to bit postion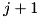 only if the probability 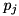of the partially constructed differential $(da[j:k], db[j:k] \rightarrow dc[j:k])$ multiplied by the bound of the probability until the end is bigger than the best probability found so far i.e. if: $B[j+1] A_{j} A_{j-1} \ldots A_{k} C^{i}_{k-1} > p_{\mathrm{max}}$
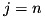    - When update the max.: $p_{\mathrm{max}} \leftarrow p_{n-1} = \mathrm{dp}(da[n-1:k],db[n-1:k] \rightarrow dc[n-1:k])$ .
  - At the end of the recursion set $B[k][i] \leftarrow p_{\mathrm{max}}$ .

Meaning of the bounds B:

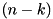$B[k][i]$ is an upper bound on on the maximum probability of the differential $(da[n-1:k], db[n-1:k] \rightarrow dc[n-1:k])$ because clearly for any choice $dc[n-1:k]$ of the $(n-k)$ MS bits of dc, the probability 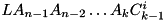$L A_{n-1} A_{n-2} \ldots A_{k} C^i_{k-1}$ will never be bigger than . 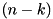Furthermore, let $G[k] = L A_{n-1} A_{n-2} \ldots A_{k}$ be the multiplication of the corresponding transition probability matrices for the $(n-k)$ MS bits of dc and let $H[k-1] = A_{k-1} A_{k-2} \ldots A_{0} C^i_{k-1}$ and $H[-1] = C$ . Then $\mathrm{dp}(da,db \rightarrow dc) = G[k] H[k-1] \le B[k] H[k-1]$ for any choice of $dc[n-1:k]$ . 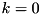In particular, when $k = 0$ $\mathrm{dp}(da,db \rightarrow dc) = \mathrm{max}_{dc}~\mathrm{dp}(da,db \rightarrow dc) = G[0] C = B[0] C$ .

See Also: max_adp_xor_i

double max_adp_xor_exper	(	gsl_matrix *	A[2][2][2],
		const WORD_T	da,
		const WORD_T	db,
		WORD_T *	dc_max
	)

Compute the maximum differential probability by exhaustive search over all output differences. Complexity: 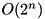$O(2^n)$ .

Parameters

A	transition probability matrices.
da	first input difference.
db	second input difference.
dc_max	maximum probability output difference.

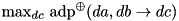Returns: $\mathrm{max}_{dc}~\mathrm{adp}^{\oplus}(da,db \rightarrow dc)$ .

See Also: max_adp_xor

void max_adp_xor_i	(	const WORD_T	i,
		const WORD_T	k,
		const WORD_T	n,
		double *	p,
		WORD_T *	dd,
		gsl_matrix *	A[2][2][2],
		gsl_vector *	B[WORD_SIZE+1],
		gsl_vector *	C,
		const WORD_T	da,
		const WORD_T	db,
		WORD_T *	dd_max,
		double *	p_max,
		WORD_T	A_size
	)

Compute an upper bound $B[k][i]$ on the maximum probability of the differential $(da[n-1:k], db[n-1:k] \rightarrow dc[n-1:k])$ starting from initial state i of the S-function i.e. 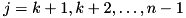$\mathrm{dp}(da[n-1:k],db[n-1:k] \rightarrow dc[n-1:k]) = L A_{n-1} A_{n-2} \ldots A_{k} C^{i}_{k-1}$ , given the upper bounds on the probabilities of the differentials $(da[n-1:j], db[n-1:j] \rightarrow dc[n-1:j])$ for $j = k+1, k+2, \ldots, n-1$ , where $L = [1~1~\ldots~1]$ is a row vector of size A_size and 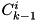$C^{i}_{k-1}$ is a unit column vector of size A_size with 1 at position 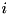$i$ and $C^{i}_{-1} = C$ .

Parameters

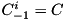i	index of the state of the S-function: `A_size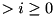` $> i \ge 0$ .
k	current bit position: 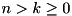$n > k \ge 0$ .
n	word size.
p	the estimated probability at bit position `k`.
dd	output difference.
A	transition probability matrices.
B	array of size `A_size` rows by (`n` + 1) columns containing upper bounds on the maximum probabilities of all `j` bit differentials 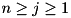$n \ge j \ge 1$ beginning from any state `i:` `A_size` $> i \ge 0$ .
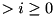C	unit row vector of size `A_size` rows, initialized with 1 at state index `i`.
da	first input difference.
db	second input difference.
dd_max	maximum probability output difference.
p_max	the maximum probability.
A_size	size of the square transition probability matrices (equivalently, the number of states of the S-function).

Algorithm Outline:

Recursively assign values to the bits of the output difference dc starting at bit popsition 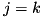$j = k$ and terminating at bit position n. The recursion proceeds to bit postion 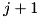$j + 1$ only if the probability 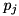$p_j$ of the partially constructed differential $(da[j:k], db[j:k] \rightarrow dc[j:k])$ multiplied by the bound of the probability until the end $B[j+1]$ is bigger than the best probability found so far i.e. if: $B[j+1] A_{j} A_{j-1} \ldots A_{k} C^{i}_{k-1} > p_{\mathrm{max}}$ . 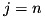When $j = n$ update the max.: $p_{\mathrm{max}} \leftarrow p_{n-1} = \mathrm{dp}(da[n-1:k],db[n-1:k] \rightarrow dc[n-1:k])$ .

See Also: max_adp_xor_bounds

Functions

Detailed Description

Function Documentation