The expected additive differential probability (EADP) of the F-function of TEA, averaged over all round keys and constants: 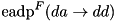$\mathrm{eadp}^{F}(da \rightarrow dd)$ . Complexity: 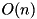$O(n)$ . More...

#include "common.hh"
#include "adp-xor3.hh"
#include "max-adp-xor3-set.hh"
#include "adp-shift.hh"
#include "tea.hh"
#include "eadp-tea-f.hh"

Functions
double	eadp_tea_f_exper (const uint32_t dx, const uint32_t dy, uint32_t lsh_const, uint32_t rsh_const)

double	eadp_tea_f (gsl_matrix A[2][2][2][2], const uint32_t da, const uint32_t db, double prob_db, uint32_t lsh_const, uint32_t rsh_const)

double	max_eadp_tea_f (gsl_matrix A[2][2][2][2], const uint32_t da, uint32_t dd_max, double *prob_max, uint32_t lsh_const, uint32_t rsh_const)

double	max_eadp_tea_f_exper (gsl_matrix A[2][2][2][2], const uint32_t da, uint32_t dd_max, double *prob_max, uint32_t lsh_const, uint32_t rsh_const)

void	nz_eadp_tea_f_i (const uint32_t k, const uint32_t n, gsl_matrix A[2][2][2][2], gsl_vector C, const uint32_t da, const uint32_t db, const uint32_t dc, uint32_t dd, double p, double p_thres, uint32_t ret_dd, double ret_p, uint32_t cnt, uint32_t max_cnt)

double	nz_eadp_tea_f (gsl_matrix A[2][2][2][2], double p_thres, uint32_t da, uint32_t ret_dd)

Detailed Description

The expected additive differential probability (EADP) of the F-function of TEA, averaged over all round keys and constants: 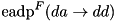$\mathrm{eadp}^{F}(da \rightarrow dd)$ . Complexity: $O(n)$ .

Author: V.Velichkov, vesse.nosp@m.lin..nosp@m.velic.nosp@m.hkov.nosp@m.@uni..nosp@m.lu

Function Documentation

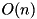double eadp_tea_f	(	gsl_matrix *	A[2][2][2][2],
		const uint32_t	da,
		const uint32_t	db,
		double *	prob_db,
		uint32_t	lsh_const,
		uint32_t	rsh_const
	)

Computing the expected additive differential probability (EADP) of the F-function of TEA, averaged over all round keys and constants. For fixed input and output differences resp. da and db, it is defined as:

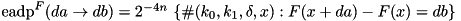$\mathrm{eadp}^{F}(da \rightarrow db) = 2^{-4n}~\{\#(k_0,k_1,\delta,x) : F(x + da) - F(x) = db\}$ .

Complexity: 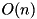$O(n)$ .

Algorithm sketch: 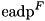$\mathrm{eadp}^{F}$ is computed as the multiplication of ADP-s of the two non-linear (w.r.t. ADD differences) components of F, namely XOR and LSH:

$\mathrm{eadp}^{F}(da \rightarrow db) = (\sum^3_{i=0} (\mathrm{adp}^{\gg 5}(da, dc_i)))~ \cdot~ \mathrm{adp}^{3\oplus}_{\mathrm{SET}}((da \ll 4), da, \{dc_0, dc_1, dc_2, dc_3\} \rightarrow db)$

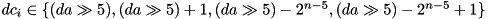where $dc_i \in \{(da \gg 5), (da \gg 5) + 1, (da \gg 5) - 2^{n-5}, (da \gg 5) - 2^{n-5} + 1\}$ are the four possible ADD differences after RSH (see adp_rsh) and 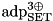$\mathrm{adp}^{3\oplus}_{\mathrm{SET}}$ is the ADP of XOR with three inputs where one of the inputs may satisfy any difference from a given set (max_adp_xor3_set).

Parameters

A	transition probability matrices for $\mathrm{adp}^{3\oplus}$ (adp_xor3_sf).
da	input difference.
db	output difference.
prob_db	the expected DP of F.
lsh_const	LSH constant.
rsh_const	RSH constant.

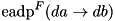Returns: $\mathrm{eadp}^{F}(da \rightarrow db)$ .

double eadp_tea_f_exper	(	const uint32_t	dx,
		const uint32_t	dy,
		uint32_t	lsh_const,
		uint32_t	rsh_const
	)

Computing the expected additive differential probability (EADP) of the F-function of TEA (see eadp_tea_f), experimentally over all round keys and constants.

Complexity: 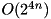$O(2^{4n})$ .

Parameters

dx	input difference.
dy	output difference.
lsh_const	LSH constant.
rsh_const	RSH constant.

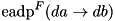Returns: $\mathrm{eadp}^{F}(da \rightarrow db)$ .

See Also: eadp_tea_f

double max_eadp_tea_f	(	gsl_matrix *	A[2][2][2][2],
		const uint32_t	da,
		uint32_t *	dd_max,
		double *	prob_max,
		uint32_t	lsh_const,
		uint32_t	rsh_const
	)

For fixed input difference da, compute an output difference dd that has maximum expected additive differential probability (EADP) averaged over all round keys and constants of the F-function of TEA:

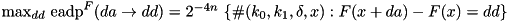$\mathrm{max}_{dd}~\mathrm{eadp}^{F}(da \rightarrow dd) = 2^{-4n}~\{\#(k_0,k_1,\delta,x) : F(x + da) - F(x) = dd\}$ .

Complexity: 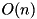$O(n)$ .

Algorithm sketch: 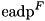$\mathrm{eadp}^{F}$ is computed as the multiplication of ADP-s of the two non-linear (w.r.t. XOR differences) components of F, namely XOR and LSH:

$\mathrm{eadp}^{F}(da \rightarrow dd) = (\sum^3_{i=0} (\mathrm{adp}^{\gg 5}(da, dc_i)))~ \cdot~ \mathrm{max}_{dd}~\mathrm{adp}^{3\oplus}_{\mathrm{SET}}((da \ll 4), da, \{dc_0, dc_1, dc_2, dc_3\} \rightarrow dd)$

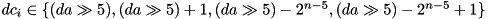where $dc_i \in \{(da \gg 5), (da \gg 5) + 1, (da \gg 5) - 2^{n-5}, (da \gg 5) - 2^{n-5} + 1\}$ are the four possible ADD differences after RSH (see adp_rsh) and 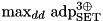$\mathrm{max}_{dd}~\mathrm{adp}^{3\oplus}_{\mathrm{SET}}$ is the maximum ADP over all outpt differences, of XOR with three inputs where one of the inputs may satisfy any difference from a given set (max_adp_xor3_set).

Parameters

A	transition probability matrices for $\mathrm{adp}^{3\oplus}$ (adp_xor3_sf).
da	input difference.
dd_max	maximum probability output difference.
prob_max	maximum expected DP of F over all output differences.
lsh_const	LSH constant.
rsh_const	RSH constant.

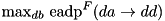Returns: $\mathrm{max}_{db}~\mathrm{eadp}^{F}(da \rightarrow dd)$ .

double max_eadp_tea_f_exper	(	gsl_matrix *	A[2][2][2][2],
		const uint32_t	da,
		uint32_t *	dd_max,
		double *	prob_max,
		uint32_t	lsh_const,
		uint32_t	rsh_const
	)

Computing the maximum expected additive differential probability (EADP) of the F-function of TEA (see eadp_tea_f), experimentally over all round keys, round constants and output differences.

Complexity: 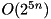$O(2^{5n})$ .

Parameters

A	transition probability matrices for $\mathrm{adp}^{3\oplus}$ (adp_xor3_sf).
da	input difference.
dd_max	output difference.
prob_max	the maximum expected DP of F.
lsh_const	LSH constant.
rsh_const	RSH constant.

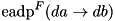Returns: $\mathrm{eadp}^{F}(da \rightarrow db)$ .

See Also: max_eadp_tea_f

double nz_eadp_tea_f	(	gsl_matrix *	A[2][2][2][2],
		double	p_thres,
		uint32_t	da,
		uint32_t *	ret_dd
	)

For fixed input diffference da to the TEA F-function, generate an arbitrary output difference dd for which the expected DP of F is above a fixed threshold i.e. 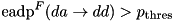$\mathrm{eadp}^{F}(da \rightarrow dd) > p_{\mathrm{thres}}$ .

Parameters

A	transition probability matrices for $\mathrm{adp}^{3\oplus}$ (adp_xor3_sf).
p_thres	probability threshold.
da	first input difference to XOR3.
ret_dd	output difference that is returned as result.

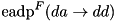Returns: $\mathrm{eadp}^{F}(da \rightarrow dd)$ .

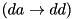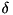Attention: Although the resulting differential $(da \rightarrow dd)$ is guaranteed to have expected probability, averaged over all keys and constants, strictly bigger than zero, its probability may still be zero for some fixed value of the round keys and $\delta$ constants.

See Also: nz_eadp_tea_f_i

void nz_eadp_tea_f_i	(	const uint32_t	k,
		const uint32_t	n,
		gsl_matrix *	A[2][2][2][2],
		gsl_vector *	C,
		const uint32_t	da,
		const uint32_t	db,
		const uint32_t	dc,
		uint32_t *	dd,
		double *	p,
		double *	p_thres,
		uint32_t *	ret_dd,
		double *	ret_p,
		uint32_t *	cnt,
		uint32_t	max_cnt
	)

For fixed input diffferences da, db and dc, to the XOR operation with three inputs in the TEA F-function, generate an arbitrary output difference dd for which the expected DP of F is nonzero i.e. 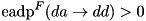$\mathrm{eadp}^{F}(da \rightarrow dd) > 0$ .

Complexity c: 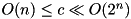$O(n) \le c \ll O(2^n)$ .

Algorithm sketch:

The function works recursively starting from the LS bit k = 0 and terminating at the MS bit n. At every bit position i it assigns values to the i-th bit of the output difference dd and evaluates the probability of the resulting partial (i+1)-bit differential: $(da[i:0], db[i:0], dc[i:0] \rightarrow dd[i:0])$ . The recursion proceeds only if this probability is not less than the threshold p_thres. 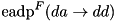When i = n, the difference $dd[n-1:0]$ is stored as the result and the probability $\mathrm{eadp}^{F}(da \rightarrow dd)$ is returned.

Note: Note that the threshold p_thres is initialized to 0.0, but is dynamically updated during the execution as soon as a higher value is found.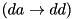

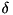Attention: Although the resulting differential $(da \rightarrow dd)$ is guaranteed to have expected probability, averaged over all keys and constants, strictly bigger than zero, its probability may still be zero for some fixed value of the round keys and $\delta$ constants.

Parameters

k	current bit position in the recursion.
n	word size.
A	transition probability matrices for $\mathrm{adp}^{3\oplus}$ (adp_xor3_sf).
C	unit column vector for computing $\mathrm{adp}^{3\oplus}$ (adp_xor3).
da	first input difference to XOR3.
db	second input difference to XOR3.
dc	third input difference to XOR3.
dd	output difference from XOR3 (and F).
p	probability of the differential $(da[k:0], db[k:0], dc[k:0] \rightarrow dd[k:0])$ .
p_thres	probability threshold.
ret_dd	output difference that is returned as result.
ret_p	the EDP 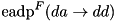$\mathrm{eadp}^{F}(da \rightarrow dd)$ .
cnt	number of output differences generated so far.
max_cnt	maximum number of output differences allowed (typically 1).

See Also: adp_xor_ddt

Functions

Detailed Description

Function Documentation