 |
YAARX: Yet Another ARX Toolkit
0.1
|
 |
YAARX: Yet Another ARX Toolkit
0.1
|
Computing an ADD partial difference distribution table (pDDT) for the F-function of block cipher XTEA. More...
#include "common.hh"#include "adp-xor.hh"#include "max-adp-xor.hh"#include "max-adp-xor-fi.hh"#include "adp-shift.hh"#include "tea-f-add-pddt.hh"#include "xtea.hh"#include "adp-xtea-f-fk.hh"Functions | |
| void | xtea_f_add_pddt_i (const uint32_t k, const uint32_t n, const uint32_t key, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const, gsl_matrix *A[2][2][2], gsl_matrix *AA[2][2][2], gsl_vector *C, uint32_t *da, uint32_t *db, uint32_t *dc, uint32_t *dd, double *p, const double p_thres, std::set< differential_t, struct_comp_diff_dx_dy > *diff_set_dx_dy) |
| void | xtea_f_add_pddt (uint32_t n, double p_thres, uint32_t lsh_const, uint32_t rsh_const, gsl_matrix *A[2][2][2], gsl_matrix *AA[2][2][2], gsl_vector *C, uint32_t key, uint32_t delta, std::set< differential_t, struct_comp_diff_dx_dy > *diff_set_dx_dy) |
| void | xtea_add_pddt_dxy_to_dp (std::multiset< differential_t, struct_comp_diff_p > *diff_mset_p, const std::set< differential_t, struct_comp_diff_dx_dy > diff_set_dx_dy) |
Computing an ADD partial difference distribution table (pDDT) for the F-function of block cipher XTEA.
| void xtea_add_pddt_dxy_to_dp | ( | std::multiset< differential_t, struct_comp_diff_p > * | diff_mset_p, |
| const std::set< differential_t, struct_comp_diff_dx_dy > | diff_set_dx_dy | ||
| ) |
From a pDDT represented in the from of a set of differentials ordered by index, compute a pDDT as a set of differentials ordered by probability.
| diff_mset_p | output pDDT: set of differentials  ordered by probability; stored in an STL multiset structure, internally implemented as a Red-Black binary search tree. ordered by probability; stored in an STL multiset structure, internally implemented as a Red-Black binary search tree. |
| diff_set_dx_dy | input pDDT: set of differentials  ordered by index ordered by index 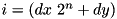 ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. |
| void xtea_f_add_pddt | ( | uint32_t | n, |
| double | p_thres, | ||
| uint32_t | lsh_const, | ||
| uint32_t | rsh_const, | ||
| gsl_matrix * | A[2][2][2], | ||
| gsl_matrix * | AA[2][2][2], | ||
| gsl_vector * | C, | ||
| uint32_t | key, | ||
| uint32_t | delta, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | diff_set_dx_dy | ||
| ) |
Compute a partial DDT (pDDT) for the XTEA F-function: wrapper function of xtea_f_add_pddt_i . By definition a pDDT contains only differentials that have probability above a fixed probability thershold.
| n | word size (default is WORD_SIZE). |
| p_thres | probability threshold (default is XTEA_ADD_P_THRES). |
| lsh_const | LSH constant (TEA_LSH_CONST). |
| rsh_const | RSH constant (TEA_RSH_CONST). |
| A | transition probability matrices for 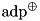 (adp_xor_sf). (adp_xor_sf). |
| AA | transition probability matrices for XOR with fixed input 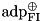 (adp_xor_fixed_input_sf). (adp_xor_fixed_input_sf). |
| C | unit column vector for computing 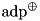 (adp_xor). (adp_xor). |
| key | round key. |
| delta | round constant. |
| diff_set_dx_dy | set of differentials  in the pDDT ordered by index in the pDDT ordered by index 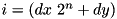 ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. |
| void xtea_f_add_pddt_i | ( | const uint32_t | k, |
| const uint32_t | n, | ||
| const uint32_t | key, | ||
| const uint32_t | delta, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const, | ||
| gsl_matrix * | A[2][2][2], | ||
| gsl_matrix * | AA[2][2][2], | ||
| gsl_vector * | C, | ||
| uint32_t * | da, | ||
| uint32_t * | db, | ||
| uint32_t * | dc, | ||
| uint32_t * | dd, | ||
| double * | p, | ||
| const double | p_thres, | ||
| std::set< differential_t, struct_comp_diff_dx_dy > * | diff_set_dx_dy | ||
| ) |
Computes an ADD partial difference distribution table (pDDT) for the F-function of block cipher TEA.
| k | current bit position in the recursion. |
| n | word size (default is WORD_SIZE). |
| key | round key. |
| delta | round constant. |
| lsh_const | LSH constant (TEA_LSH_CONST). |
| rsh_const | RSH constant (TEA_RSH_CONST). |
| A | transition probability matrices for XOR 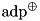 (adp_xor_sf). (adp_xor_sf). |
| AA | transition probability matrices for XOR with fixed input 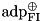 (adp_xor_fixed_input_sf). (adp_xor_fixed_input_sf). |
| C | unit column vector for computing 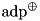 (adp_xor). (adp_xor). |
| da | input difference to the F-function of XTEA. |
| db | output difference from the LSH operation in F. |
| dc | output difference from the RSH operation in F. |
| dd | output difference from the XOR operation in F. |
| p | probability of the partially constructed differential ![$(db[k:0], dc[k:0] \rightarrow dd[k:0])$](form_502.png) for the XOR operation in F. for the XOR operation in F. |
| p_thres | probability threshold (default is XTEA_ADD_P_THRES). |
| diff_set_dx_dy | set of differentials  in the pDDT ordered by index in the pDDT ordered by index 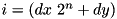 ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. ; stored in an STL set structure, internally implemented as a Red-Black binary search tree. |
Algorithm Outline:
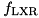 component of the F-function of XTEA (see xtea_f_lxr):
component of the F-function of XTEA (see xtea_f_lxr): 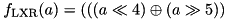 . Note that when doing this, we treat the two inputs
. Note that when doing this, we treat the two inputs 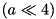 and
and 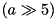 as independent inputs, denoted respectively by
as independent inputs, denoted respectively by 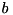 and
and 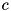 . At every bit position in the recursion we require the corresponding partially constructed input differences
. At every bit position in the recursion we require the corresponding partially constructed input differences 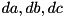 and the output difference
and the output difference 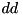 to satisfy conditions lsh_condition_is_sat and rsh_condition_is_sat. As a result, after the MSB is processed and
to satisfy conditions lsh_condition_is_sat and rsh_condition_is_sat. As a result, after the MSB is processed and 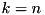 the so constructed differences satisfy the following constions (see tea_f_add_pddt_i):
the so constructed differences satisfy the following constions (see tea_f_add_pddt_i):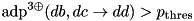 .
.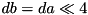 .
.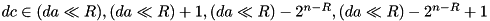 , so that
, so that 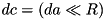 where
where 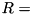 TEA_RSH_CONST.
TEA_RSH_CONST.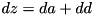 according to the feed-forward operation in F (see xtea_f) and compute the maximum probability output difference
according to the feed-forward operation in F (see xtea_f) and compute the maximum probability output difference 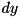 for the ADD operation with round key and
for the ADD operation with round key and 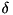 (see xtea_f) with one fixed input:
(see xtea_f) with one fixed input: 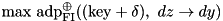 .
.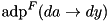 to the full function F using adp_xtea_f_approx . Set the adjusted probability to
to the full function F using adp_xtea_f_approx . Set the adjusted probability to 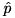 .
.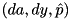 in the pDDT.
in the pDDT.