The XOR differential probability (XDP) of the F-function of TEA for a fixed key and round constants: 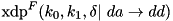$\mathrm{xdp}^{F}(k_0, k_1, \delta |~ da \rightarrow dd)$ . More...

#include "common.hh"
#include "tea.hh"

Functions
double	xdp_f_fk_exper (const uint32_t da, const uint32_t db, const uint32_t k0, const uint32_t k1, const uint32_t delta, uint32_t lsh_const, uint32_t rsh_const)

double	max_xdp_f_fk_dx_exper (uint32_t *max_dx, const uint32_t dy, const uint32_t k0, const uint32_t k1, const uint32_t delta, uint32_t lsh_const, uint32_t rsh_const)

double	max_xdp_f_fk_dy_exper (const uint32_t dx, uint32_t *max_dy, const uint32_t k0, const uint32_t k1, const uint32_t delta, uint32_t lsh_const, uint32_t rsh_const)

bool	xdp_f_is_sat (const uint32_t mask_i, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t k0, const uint32_t k1, const uint32_t delta, const uint32_t dx, const uint32_t dy, int32_t x)

bool	xdp_f_check_x (const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t k0, const uint32_t k1, const uint32_t delta, const uint32_t dx, const uint32_t dy, const uint32_t x)

uint32_t	xdp_f_assign_bit_x (const uint32_t n, const uint32_t i, const uint32_t mask_i, const uint32_t x, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t k0, const uint32_t k1, const uint32_t delta, const uint32_t dx, const uint32_t dy, uint32_t x_cnt, double prob)

double	xdp_f_fk (const uint32_t n, const uint32_t dx, const uint32_t dy, const uint32_t k0, const uint32_t k1, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const)

uint32_t	xdp_f_assign_bit_x_dx (const uint32_t n, const uint32_t i, const uint32_t mask_i, const uint32_t x, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t k0, const uint32_t k1, const uint32_t delta, const uint32_t dx, const uint32_t dy, uint64_t x_cnt, double ret_prob, uint32_t *ret_dx)

double	max_dx_xdp_f_fk (const uint32_t n, uint32_t *ret_dx, const uint32_t dy, const uint32_t k0, const uint32_t k1, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const)

uint32_t	xdp_f_assign_bit_x_dy (const uint32_t n, const uint32_t i, const uint32_t mask_i, const uint32_t x, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t k0, const uint32_t k1, const uint32_t delta, const uint32_t dx, const uint32_t dy, uint64_t x_cnt, double ret_prob, uint32_t *ret_dy)

double	max_dy_xdp_f_fk (const uint32_t n, const uint32_t dx, uint32_t *ret_dy, const uint32_t k0, const uint32_t k1, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const)

Detailed Description

The XOR differential probability (XDP) of the F-function of TEA for a fixed key and round constants: 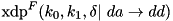$\mathrm{xdp}^{F}(k_0, k_1, \delta |~ da \rightarrow dd)$ .

Author: V.Velichkov, vesse.nosp@m.lin..nosp@m.velic.nosp@m.hkov.nosp@m.@uni..nosp@m.lu

Attention: The algorithms in this file have complexity that depends on the input and output differences to F. It is worst-case exponential in the word size, but is sub-exponential on average.

Function Documentation

double max_dx_xdp_f_fk	(	const uint32_t	n,
		uint32_t *	ret_dx,
		const uint32_t	dy,
		const uint32_t	k0,
		const uint32_t	k1,
		const uint32_t	delta,
		const uint32_t	lsh_const,
		const uint32_t	rsh_const
	)

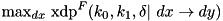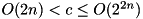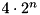For given output difference dy, compute the maximum probability input differences dx over all input differences: $\mathrm{max}_{dx} ~\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ . Complexity: $O(2n) < c \le O(2^{2n})$ . Memory: $4 \cdot 2^n$ Bytes.

Parameters

n	word size.
ret_dx	maximum probability input difference.
dy	output difference.
k0	first round key.
k1	second round key.
delta	round constant.
lsh_const	LSH constant.
rsh_const	RSH constant.

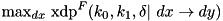Returns: $\mathrm{max}_{dx} ~\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ .

See Also: xdp_f_assign_bit_x_dx

double max_dy_xdp_f_fk	(	const uint32_t	n,
		const uint32_t	dx,
		uint32_t *	ret_dy,
		const uint32_t	k0,
		const uint32_t	k1,
		const uint32_t	delta,
		const uint32_t	lsh_const,
		const uint32_t	rsh_const
	)

For given input difference dx, compute the maximum probability output difference dy over all output differences: 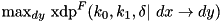$\mathrm{max}_{dy} ~\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ . Complexity: 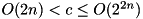$O(2n) < c \le O(2^{2n})$ . Memory requirement: 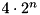$4 \cdot 2^n$ Bytes.

Parameters

n	word size.
dx	input difference.
ret_dy	maximum probability output difference.
k0	first round key.
k1	second round key.
delta	round constant.
lsh_const	LSH constant.
rsh_const	RSH constant.

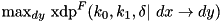Returns: $\mathrm{max}_{dy} ~\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ .

See Also: xdp_f_assign_bit_x_dy, max_dy_xdp_f_fk

double max_xdp_f_fk_dx_exper	(	uint32_t *	max_dx,
		const uint32_t	dy,
		const uint32_t	k0,
		const uint32_t	k1,
		const uint32_t	delta,
		uint32_t	lsh_const,
		uint32_t	rsh_const
	)

For given output difference dy, compute the maximum probability input differences dx over all input differences: 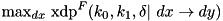$\mathrm{max}_{dx} ~\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ through exhaustive search over all input values and input differences. Complexity: $O(2^{2n})$ .

Parameters

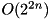max_dx	maximum probability input difference.
dy	output difference.
k0	first round key.
k1	second round key.
delta	round constant.
lsh_const	LSH constant.
rsh_const	RSH constant.

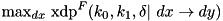Returns: $\mathrm{max}_{dx} ~\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ .

See Also: max_dx_xdp_f_fk

double max_xdp_f_fk_dy_exper	(	const uint32_t	dx,
		uint32_t *	max_dy,
		const uint32_t	k0,
		const uint32_t	k1,
		const uint32_t	delta,
		uint32_t	lsh_const,
		uint32_t	rsh_const
	)

For given input difference dx, compute the maximum probability output difference dy over all output differences: 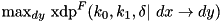$\mathrm{max}_{dy} ~\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ through exhaustive search over all input values and input differences. Complexity: $O(2^{2n})$ .

Parameters

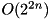dx	input difference.
max_dy	maximum probability output difference.
k0	first round key.
k1	second round key.
delta	round constant.
lsh_const	LSH constant.
rsh_const	RSH constant.

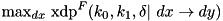Returns: $\mathrm{max}_{dx} ~\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ .

See Also: max_dy_xdp_f_fk

uint32_t xdp_f_assign_bit_x	(	const uint32_t	n,
		const uint32_t	i,
		const uint32_t	mask_i,
		const uint32_t	x,
		const uint32_t	lsh_const,
		const uint32_t	rsh_const,
		const uint32_t	k0,
		const uint32_t	k1,
		const uint32_t	delta,
		const uint32_t	dx,
		const uint32_t	dy,
		uint32_t *	x_cnt,
		double *	prob
	)

Counts the number of values x for which the differential $(dx \rightarrow dy)$ for the F-function of TEA is satisfied. The function operates by recursively assigning the bits of x starting from bit position i and terminating at the MS bit n. The recursion proceeds to bit 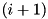$(i+1)$ only if the differential is satisfied on the i LS bits. This is checked by applying xdp_f_is_sat.

Parameters

n	word size (terminating bit popsition).
i	current bit position.
mask_i	mask on the `i` LS bits of `x`.
x	input value of size at least (`i` + `rsh_const`).
lsh_const	LSH constant.
rsh_const	RSH constant.
k0	first round key.
k1	second round key.
delta	round constant.
dx	input difference.
dy	output difference.
x_cnt	number of values satisfying $(dx \rightarrow dy)$ .
prob	the fixed-key XOR probability of `F: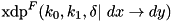` $\mathrm{xdp}^{F}(k_0, k_1, \delta \|~ dx \rightarrow dy)$ .

Returns: 1 if satisfies $(dx[i-1:0] \rightarrow dy[i-1:0])$ ; 0 otherwise.

See Also: xdp_f_fk

uint32_t xdp_f_assign_bit_x_dx	(	const uint32_t	n,
		const uint32_t	i,
		const uint32_t	mask_i,
		const uint32_t	x,
		const uint32_t	lsh_const,
		const uint32_t	rsh_const,
		const uint32_t	k0,
		const uint32_t	k1,
		const uint32_t	delta,
		const uint32_t	dx,
		const uint32_t	dy,
		uint64_t *	x_cnt,
		double *	ret_prob,
		uint32_t *	ret_dx
	)

For given output difference dy, compute all input differences dx and their probabilities, by counting all values x that satisfy the differential $(dx \rightarrow dy)$ for a fixed key and round constant. At the same time keeps track of the maximum probability input difference.

The function works by recursively assigning the bits of x and dx starting at bit position i and terminating at the MS bit n. The recursion proceeds to bit 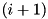$(i+1)$ only if the differential is satisfied on the i LS bits. This is checked by applying xdp_f_is_sat .

Parameters

n	word size (terminating bit popsition).
i	current bit position.
mask_i	mask on the `i` LS bits of `x`.
x	input value of size at least (`i` + `rsh_const`).
lsh_const	LSH constant.
rsh_const	RSH constant.
k0	first round key.
k1	second round key.
delta	round constant.
dx	input difference.
dy	output difference.
x_cnt	array of 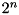counters - each one keeps track of the number of values satisfying $(dx \rightarrow dy)$ for every `dx`.
ret_prob	the maximum probability over all input differences 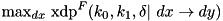$\mathrm{max}_{dx} ~\mathrm{xdp}^{F}(k_0, k_1, \delta \|~ dx \rightarrow dy)$ .
ret_dx	the input difference that has maximum probability.

Returns: 1 if satisfies $(dx[i-1:0] \rightarrow dy[i-1:0])$ ; 0 otherwise.

See Also: xdp_f_assign_bit_x, max_dx_xdp_f_fk

uint32_t xdp_f_assign_bit_x_dy	(	const uint32_t	n,
		const uint32_t	i,
		const uint32_t	mask_i,
		const uint32_t	x,
		const uint32_t	lsh_const,
		const uint32_t	rsh_const,
		const uint32_t	k0,
		const uint32_t	k1,
		const uint32_t	delta,
		const uint32_t	dx,
		const uint32_t	dy,
		uint64_t *	x_cnt,
		double *	ret_prob,
		uint32_t *	ret_dy
	)

For given input difference dx, compute all output differences dy and their probabilities, by counting all values x that satisfy the differential $(dx \rightarrow dy)$ for a fixed key and round constant. At the same time keeps track of the maximum probability output difference.

The function works by recursively assigning the bits of x and dy starting at bit position i and terminating at the MS bit n. The recursion proceeds to bit 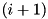$(i+1)$ only if the differential is satisfied on the i LS bits. This is checked by applying xdp_f_is_sat.

Parameters

n	word size (terminating bit popsition).
i	current bit position.
mask_i	mask on the `i` LS bits of `x`.
x	input value of size at least (`i` + `rsh_const`).
lsh_const	LSH constant.
rsh_const	RSH constant.
k0	first round key.
k1	second round key.
delta	round constant.
dx	input difference.
dy	output difference.
x_cnt	array of 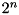counters - each one keeps track of the number of values satisfying $(dx \rightarrow dy)$ for every `dy`.
ret_prob	the maximum probability over all output differences 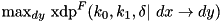$\mathrm{max}_{dy} ~\mathrm{xdp}^{F}(k_0, k_1, \delta \|~ dx \rightarrow dy)$ .
ret_dy	the output difference that has maximum probability.

Returns: 1 if satisfies $(dx[i-1:0] \rightarrow dy[i-1:0])$ ; 0 otherwise.

See Also: xdp_f_assign_bit_x_dx

bool xdp_f_check_x	(	const uint32_t	lsh_const,
		const uint32_t	rsh_const,
		const uint32_t	k0,
		const uint32_t	k1,
		const uint32_t	delta,
		const uint32_t	dx,
		const uint32_t	dy,
		const uint32_t	x
	)

Check if a given value x satisfies the XOR differential $(dx \rightarrow dy)$ for the TEA F-function.

Parameters

lsh_const	LSH constant.
rsh_const	RSH constant.
k0	first round key.
k1	second round key.
delta	round constant.
dx	input difference.
dy	output difference.
x	input value.

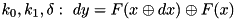Returns: TRUE if $k_0, k_1, \delta:~ dy = F(x \oplus dx) \oplus F(x)$ .

double xdp_f_fk	(	const uint32_t	n,
		const uint32_t	dx,
		const uint32_t	dy,
		const uint32_t	k0,
		const uint32_t	k1,
		const uint32_t	delta,
		const uint32_t	lsh_const,
		const uint32_t	rsh_const
	)

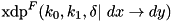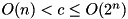Compute the fixed-key, fixed-constant XOR differential probability of the F-function of block cipher TEA: $\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ . Complexity: $O(n) < c \le O(2^n)$ .

Parameters

n	word size.
dx	input difference.
dy	output difference.
k0	first round key.
k1	second round key.
delta	round constant.
lsh_const	LSH constant.
rsh_const	RSH constant.

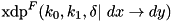Returns: $\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ .

See Also: xdp_f_assign_bit_x

double xdp_f_fk_exper	(	const uint32_t	da,
		const uint32_t	db,
		const uint32_t	k0,
		const uint32_t	k1,
		const uint32_t	delta,
		uint32_t	lsh_const,
		uint32_t	rsh_const
	)

Compute the fixed-key, fixed-constant XOR differential probability of the F-function of block cipher TEA: 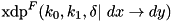$\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ through exhaustive search over all input values. Complexity: $O(2^n)$ .

Parameters

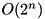da	input difference.
db	output difference.
k0	first round key.
k1	second round key.
delta	round constant.
lsh_const	LSH constant.
rsh_const	RSH constant.

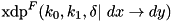Returns: $\mathrm{xdp}^{F}(k_0, k_1, \delta |~ dx \rightarrow dy)$ .

See Also: xdp_f_fk

bool xdp_f_is_sat	(	const uint32_t	mask_i,
		const uint32_t	lsh_const,
		const uint32_t	rsh_const,
		const uint32_t	k0,
		const uint32_t	k1,
		const uint32_t	delta,
		const uint32_t	dx,
		const uint32_t	dy,
		int32_t	x
	)

Check if the differential $(dx \rightarrow dy)$ for F is satisfied on the i LS bits of x i.e. check if $k_0, k_1, \delta:~ dy[i-1:0] = F(x[i-1:0] \oplus dx[i-1:0]) \oplus F(x[i-1:0])$ .

Attention: x must be of size at least 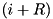bits where R is the RSH constant of F.

Parameters

mask_i	`i` bit mask.
lsh_const	LSH constant.
rsh_const	RSH constant.
k0	first round key.
k1	second round key.
delta	round constant.
dx	input difference.
dy	output difference.
x	input value of size at least (`i` + `rsh_const`).

Returns: TRUE if $k_0, k_1, \delta:~ dy[i-1:0] = F(x[i-1:0] \oplus dx[i-1:0]) \oplus F(x[i-1:0)$ .

Functions

Detailed Description

Function Documentation