 |
YAARX: Yet Another ARX Toolkit
0.1
|
 |
YAARX: Yet Another ARX Toolkit
0.1
|
The ADD differential probability of the F-function of XTEA for a fixed key and round constants 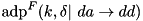 . Complexity:
. Complexity: 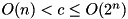 .
More...
.
More...
#include "common.hh"#include "adp-xor.hh"#include "max-adp-xor.hh"#include "adp-xor-fi.hh"#include "max-adp-xor-fi.hh"#include "adp-shift.hh"#include "xtea.hh"Functions | |
| double | adp_xtea_f_exper (const uint32_t da, const uint32_t db, const uint32_t k, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const) |
| double | adp_xtea_f_approx (const uint32_t ninputs, const uint32_t da, const uint32_t db, const uint32_t k, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const) |
| double | max_dy_adp_xtea_f_exper (const uint32_t dx, uint32_t *dy_max, const uint32_t k, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const) |
| double | max_dx_adp_xtea_f_exper (uint32_t *dx_max, const uint32_t dy, const uint32_t k, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const) |
| double | adp_xtea_f_lxr_exper (const uint32_t da, const uint32_t db, uint32_t lsh_const, uint32_t rsh_const) |
| double | adp_xtea_f_lxr_approx (const uint32_t ninputs, const uint32_t da, const uint32_t db, uint32_t lsh_const, uint32_t rsh_const) |
| bool | adp_xtea_f_lxr_check_x (const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t dx, const uint32_t dy, const uint32_t x) |
| bool | adp_xtea_f_lxr_is_sat (const uint32_t mask_i, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t dx, const uint32_t dy, int32_t x) |
| uint32_t | adp_xtea_f_lxr_assign_bit_x (const uint32_t n, const uint32_t i, const uint32_t mask_i, const uint32_t x, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t dx, const uint32_t dy, uint32_t *x_cnt, double *prob) |
| double | adp_xtea_f_lxr (const uint32_t n, const uint32_t dx, const uint32_t dy, const uint32_t lsh_const, const uint32_t rsh_const) |
| double | adp_xtea_f_approx (const uint32_t n, gsl_matrix *A[2][2][2], const uint32_t dx, const uint32_t dy, const uint32_t k, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const) |
| bool | adp_xtea_f_check_x (const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t k, const uint32_t delta, const uint32_t dx, const uint32_t dy, const uint32_t x) |
| bool | adp_xtea_f_is_sat (const uint32_t mask_i, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t k, const uint32_t delta, const uint32_t dx, const uint32_t dy, const uint32_t x) |
| uint32_t | adp_xtea_f_assign_bit_x (const uint32_t n, const uint32_t i, const uint32_t mask_i, const uint32_t x, const uint32_t key, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t dx, const uint32_t dy, uint32_t *x_cnt, double *prob) |
| uint32_t | adp_xtea_f_assign_bit_x_dx (const uint32_t n, const uint32_t i, const uint32_t mask_i, const uint32_t x, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t key, const uint32_t delta, const uint32_t dx, const uint32_t dy, uint64_t *x_cnt, double *ret_prob, uint32_t *ret_dx) |
| uint32_t | adp_xtea_f_assign_bit_x_dy (const uint32_t n, const uint32_t i, const uint32_t mask_i, const uint32_t x, const uint32_t lsh_const, const uint32_t rsh_const, const uint32_t key, const uint32_t delta, const uint32_t dx, const uint32_t dy, uint64_t *x_cnt, double *ret_prob, uint32_t *ret_dy) |
| double | adp_xtea_f (const uint32_t n, const uint32_t dx, const uint32_t dy, const uint32_t key, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const) |
| double | max_dy_adp_xtea_f (const uint32_t n, const uint32_t dx, uint32_t *ret_dy, const uint32_t key, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const) |
| double | max_dx_adp_xtea_f (const uint32_t n, uint32_t *ret_dx, const uint32_t dy, const uint32_t key, const uint32_t delta, const uint32_t lsh_const, const uint32_t rsh_const) |
| double | first_nz_adp_xtea_f (gsl_matrix *A[2][2][2], gsl_matrix *AA[2][2][2], const uint32_t key, const uint32_t delta, const uint32_t da, uint32_t *ret_dd, uint32_t lsh_const, uint32_t rsh_const) |
The ADD differential probability of the F-function of XTEA for a fixed key and round constants 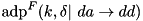 . Complexity:
. Complexity: 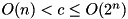 .
.
| double adp_xtea_f | ( | const uint32_t | n, |
| const uint32_t | dx, | ||
| const uint32_t | dy, | ||
| const uint32_t | key, | ||
| const uint32_t | delta, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const | ||
| ) |
Compute the fixed-key, fixed-constant ADD differential probability of the F-function of block cipher XTEA: 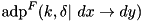 . Complexity:
. Complexity: 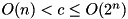 .
.
| n | word size. |
| dx | input difference. |
| dy | output difference. |
| key | round key. |
| delta | round constant. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
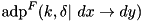 .
. | double adp_xtea_f_approx | ( | const uint32_t | ninputs, |
| const uint32_t | da, | ||
| const uint32_t | db, | ||
| const uint32_t | k, | ||
| const uint32_t | delta, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const | ||
| ) |
An approximation of the ADP of the XTEA F-function (xtea_f) obtained over a number of input chosen plaintext pairs chosen uniformly at random.
| ninputs | number of chosen plaintext pairs. |
| da | input difference. |
| db | output difference. |
| k | round key. |
| delta | round constant. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
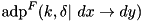 .
. | double adp_xtea_f_approx | ( | const uint32_t | n, |
| gsl_matrix * | A[2][2][2], | ||
| const uint32_t | dx, | ||
| const uint32_t | dy, | ||
| const uint32_t | k, | ||
| const uint32_t | delta, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const | ||
| ) |
An approximation of the ADD differential probability (ADP) of the XTEA F-function (xtea_f) with fixed round key and round cnstant, obtained as the multiplication the ADP of its 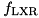 component (adp_xtea_f_lxr) and the ADP of XOR with one fixed input (adp_xor_fixed_input):
component (adp_xtea_f_lxr) and the ADP of XOR with one fixed input (adp_xor_fixed_input):
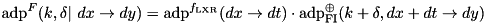 .
.
Algorithm sketch:
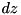 s.t.
s.t. 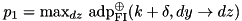 .
. 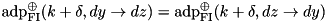 .
.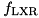 :
: 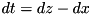 .
.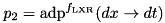 .
.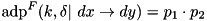 .
.| n | word size. |
| A | transition probability matrices for 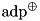 with FI (adp_xor_fixed_input_sf). with FI (adp_xor_fixed_input_sf). |
| dx | input difference. |
| dy | output difference. |
| k | round key. |
| delta | round constant. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
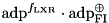 .
. | uint32_t adp_xtea_f_assign_bit_x | ( | const uint32_t | n, |
| const uint32_t | i, | ||
| const uint32_t | mask_i, | ||
| const uint32_t | x, | ||
| const uint32_t | key, | ||
| const uint32_t | delta, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const, | ||
| const uint32_t | dx, | ||
| const uint32_t | dy, | ||
| uint32_t * | x_cnt, | ||
| double * | prob | ||
| ) |
Counts the number of values x for which the differential  for the F-function of XTEA is satisfied. The function operates by recursively assigning the bits of
for the F-function of XTEA is satisfied. The function operates by recursively assigning the bits of x starting from bit position i and terminating at the MS bit n. The recursion proceeds to bit 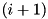 only if the differential is satisfied on the
only if the differential is satisfied on the i LS bits. This is checked by applying adp_xtea_f_is_sat.
| n | word size (terminating bit popsition). |
| i | current bit position. |
| mask_i | mask on the i LS bits of x. |
| x | input value of size at least (i + rsh_const). |
| key | round key. |
| delta | round constant. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
| dx | input difference. |
| dy | output difference. |
| x_cnt | number of values satisfying  . . |
| prob | the fixed-key ADD probability of F: 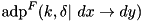 . . |
1 if ![$x[i-1:0]$](form_111.png) satisfies
satisfies ![$(dx[i-1:0] \rightarrow dy[i-1:0])$](form_112.png) ;
; 0 otherwise. | uint32_t adp_xtea_f_assign_bit_x_dx | ( | const uint32_t | n, |
| const uint32_t | i, | ||
| const uint32_t | mask_i, | ||
| const uint32_t | x, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const, | ||
| const uint32_t | key, | ||
| const uint32_t | delta, | ||
| const uint32_t | dx, | ||
| const uint32_t | dy, | ||
| uint64_t * | x_cnt, | ||
| double * | ret_prob, | ||
| uint32_t * | ret_dx | ||
| ) |
For given output difference dy, compute all input differences dx and their probabilities, by counting all values x that satisfy the differential  for a fixed key and round constant. At the same time keeps track of the maximum probability input difference.
for a fixed key and round constant. At the same time keeps track of the maximum probability input difference.
The function works by recursively assigning the bits of x and dx starting at bit position i and terminating at the MS bit n. The recursion proceeds to bit 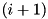 only if the differential is satisfied on the
only if the differential is satisfied on the i LS bits. This is checked by applying adp_f_is_sat .
| n | word size (terminating bit popsition). |
| i | current bit position. |
| mask_i | mask on the i LS bits of x. |
| x | input value of size at least (i + rsh_const). |
| key | round key. |
| delta | round constant. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
| dx | input difference. |
| dy | output difference. |
| x_cnt | array of 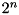 counters - each one keeps track of the number of values satisfying counters - each one keeps track of the number of values satisfying  for every for every dx. |
| ret_prob | the maximum probability over all input differences 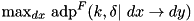 . . |
| ret_dx | the input difference that has maximum probability. |
1 if ![$x[i-1:0]$](form_111.png) satisfies
satisfies ![$(dx[i-1:0] \rightarrow dy[i-1:0])$](form_112.png) ;
; 0 otherwise.| uint32_t adp_xtea_f_assign_bit_x_dy | ( | const uint32_t | n, |
| const uint32_t | i, | ||
| const uint32_t | mask_i, | ||
| const uint32_t | x, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const, | ||
| const uint32_t | key, | ||
| const uint32_t | delta, | ||
| const uint32_t | dx, | ||
| const uint32_t | dy, | ||
| uint64_t * | x_cnt, | ||
| double * | ret_prob, | ||
| uint32_t * | ret_dy | ||
| ) |
For given input difference dx, compute all output differences dy and their probabilities, by counting all values x that satisfy the differential  for a fixed key and round constant. At the same time keeps track of the maximum probability output difference.
for a fixed key and round constant. At the same time keeps track of the maximum probability output difference.
The function works by recursively assigning the bits of x and dy starting at bit position i and terminating at the MS bit n. The recursion proceeds to bit 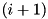 only if the differential is satisfied on the
only if the differential is satisfied on the i LS bits. This is checked by applying adp_f_is_sat.
| n | word size (terminating bit popsition). |
| i | current bit position. |
| mask_i | mask on the i LS bits of x. |
| x | input value of size at least (i + rsh_const). |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
| key | round key. |
| delta | round constant. |
| dx | input difference. |
| dy | output difference. |
| x_cnt | array of 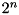 counters - each one keeps track of the number of values satisfying counters - each one keeps track of the number of values satisfying  for every for every dy. |
| ret_prob | the maximum probability over all output differences 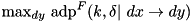 . . |
| ret_dy | the output difference that has maximum probability. |
1 if ![$x[i-1:0]$](form_111.png) satisfies
satisfies ![$(dx[i-1:0] \rightarrow dy[i-1:0])$](form_112.png) ;
; 0 otherwise.| bool adp_xtea_f_check_x | ( | const uint32_t | lsh_const, |
| const uint32_t | rsh_const, | ||
| const uint32_t | k, | ||
| const uint32_t | delta, | ||
| const uint32_t | dx, | ||
| const uint32_t | dy, | ||
| const uint32_t | x | ||
| ) |
Check if a given value x satisfies the ADD differential  for the XTEA F-function.
for the XTEA F-function.
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
| k | round key. |
| delta | round constant. |
| dx | input difference. |
| dy | output difference. |
| x | input value. |
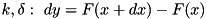 .
. | double adp_xtea_f_exper | ( | const uint32_t | da, |
| const uint32_t | db, | ||
| const uint32_t | k, | ||
| const uint32_t | delta, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const | ||
| ) |
Compute the fixed-key, fixed-constant ADD differential probability of the F-function of block cipher XTEA: 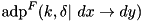 through exhaustive search over all input values. Complexity:
through exhaustive search over all input values. Complexity: 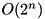 .
.
| da | input difference. |
| db | output difference. |
| k | round key. |
| delta | round constant. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
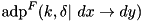 .
. | bool adp_xtea_f_is_sat | ( | const uint32_t | mask_i, |
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const, | ||
| const uint32_t | k, | ||
| const uint32_t | delta, | ||
| const uint32_t | dx, | ||
| const uint32_t | dy, | ||
| const uint32_t | x | ||
| ) |
Check if the differential  for
for F (xtea_f) is satisfied on the i LS bits of x i.e. check if
![$k, \delta:~ dy[i-1:0] = F(x[i-1:0] + dx[i-1:0]) - F(x[i-1:0]) ~\mathrm{mod} ~2^{i}$](form_160.png) .
.
x must be of size at least 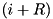 bits where
bits where R is the RSH constant of F.| mask_i | i bit mask. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
| k | round key. |
| delta | round constant. |
| dx | input difference. |
| dy | output difference. |
| x | input value of size at least (i + rsh_const). |
![$k, \delta:~ dy[i-1:0] = F(x[i-1:0] + dx[i-1:0]) - F(x[i-1:0]) ~\mathrm{mod} ~2^{i}$](form_160.png) .
. | double adp_xtea_f_lxr | ( | const uint32_t | n, |
| const uint32_t | dx, | ||
| const uint32_t | dy, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const | ||
| ) |
Compute the ADD differential probability of the 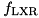 (xtea_f_lxr) function:
(xtea_f_lxr) function: 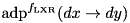 . Complexity c:
. Complexity c: 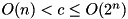 .
.
| n | word size. |
| dx | input difference. |
| dy | output difference. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
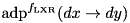 .
. | double adp_xtea_f_lxr_approx | ( | const uint32_t | ninputs, |
| const uint32_t | da, | ||
| const uint32_t | db, | ||
| uint32_t | lsh_const, | ||
| uint32_t | rsh_const | ||
| ) |
An approximation of the ADP of 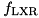 (xtea_f_lxr) obtained over a number of input chosen plaintext pairs chosen uniformly at random.
(xtea_f_lxr) obtained over a number of input chosen plaintext pairs chosen uniformly at random.
| ninputs | number of input chosen plaintext pairs. |
| da | input difference. |
| db | output difference. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
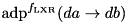
| uint32_t adp_xtea_f_lxr_assign_bit_x | ( | const uint32_t | n, |
| const uint32_t | i, | ||
| const uint32_t | mask_i, | ||
| const uint32_t | x, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const, | ||
| const uint32_t | dx, | ||
| const uint32_t | dy, | ||
| uint32_t * | x_cnt, | ||
| double * | prob | ||
| ) |
Counts the number of values x for which the differential  for the
for the 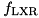 (xtea_f_lxr) function is satisfied. The algorithm works by recursively assigning the bits of
(xtea_f_lxr) function is satisfied. The algorithm works by recursively assigning the bits of x starting from bit position i and terminating at the MS bit n. The recursion proceeds to bit 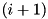 only if the differential is satisfied on the
only if the differential is satisfied on the i LS bits. This is checked by applying adp_xtea_f_lxr_is_sat.
| n | word size (terminating bit popsition). |
| i | current bit position. |
| mask_i | mask on the i LS bits of x. |
| x | input value of size at least (i + rsh_const). |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
| dx | input difference. |
| dy | output difference. |
| x_cnt | number of values satisfying  . . |
| prob | the probability 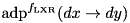 . . |
1 if ![$x[i-1:0]$](form_111.png) satisfies
satisfies ![$(dx[i-1:0] \rightarrow dy[i-1:0])$](form_112.png) ;
; 0 otherwise. | bool adp_xtea_f_lxr_check_x | ( | const uint32_t | lsh_const, |
| const uint32_t | rsh_const, | ||
| const uint32_t | dx, | ||
| const uint32_t | dy, | ||
| const uint32_t | x | ||
| ) |
Check if a given value x satisfies the ADD differential  for the function
for the function 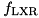 (xtea_f_lxr).
(xtea_f_lxr).
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
| dx | input difference. |
| dy | output difference. |
| x | input value. |
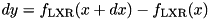 .
. | double adp_xtea_f_lxr_exper | ( | const uint32_t | da, |
| const uint32_t | db, | ||
| uint32_t | lsh_const, | ||
| uint32_t | rsh_const | ||
| ) |
Compute the ADD differential probability of the 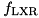 (xtea_f_lxr) component of the F-function of block cipher XTEA, through exhaustive search over all input values. Complexity:
(xtea_f_lxr) component of the F-function of block cipher XTEA, through exhaustive search over all input values. Complexity: 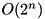 .
.
| da | input difference. |
| db | output difference. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
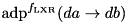
| bool adp_xtea_f_lxr_is_sat | ( | const uint32_t | mask_i, |
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const, | ||
| const uint32_t | dx, | ||
| const uint32_t | dy, | ||
| int32_t | x | ||
| ) |
Check if the differential  for the function
for the function 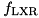 (xtea_f_lxr) is satisfied on the
(xtea_f_lxr) is satisfied on the i LS bits of x i.e. check if
![$dy[i-1:0] = f_{\mathrm{LXR}}(x[i-1:0] + dx[i-1:0]) - f_{\mathrm{LXR}}(x[i-1:0]) ~\mathrm{mod} ~2^{i}$](form_149.png) .
.
x must be of size at least 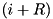 bits where
bits where R is the RSH constant of 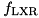 .
.| mask_i | i bit mask. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
| dx | input difference. |
| dy | output difference. |
| x | input value of size at least (i + rsh_const). |
![$dy[i-1:0] = f_{\mathrm{LXR}}(x[i-1:0] + dx[i-1:0]) - f_{\mathrm{LXR}}(x[i-1:0]) ~\mathrm{mod} ~2^{i}$](form_149.png) .
. | double first_nz_adp_xtea_f | ( | gsl_matrix * | A[2][2][2], |
| gsl_matrix * | AA[2][2][2], | ||
| const uint32_t | key, | ||
| const uint32_t | delta, | ||
| const uint32_t | da, | ||
| uint32_t * | ret_dd, | ||
| uint32_t | lsh_const, | ||
| uint32_t | rsh_const | ||
| ) |
For the XTEA F-function (xtea_f), for fixed input difference da, compute an arbitrary dd such that the differential 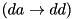 has non-zero probability.
has non-zero probability.
The procedure approximates the ADP of the TEA F-function as a multiplication of the ADP of its three non-linear components (w.r.t. ADD differences): the two XOR operations and the RSH operation (see xtea_f):
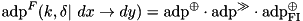
Algorithm sketch:
![$ dy: \mathrm{max}_{dc[i]}~\mathrm{adp}^{\oplus}(db, dc[i] \rightarrow dy) $](form_163.png) , where
, where ![$dc[i] \in \{(da \gg 5), (da \gg 5) + 1, (da \gg 5) - 2^{n-5}, (da \gg 5) - 2^{n-5} + 1\}$](form_164.png) , is one of the four possible ADD differences after RSH (adp_rsh).
, is one of the four possible ADD differences after RSH (adp_rsh).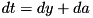 .
.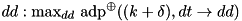 .
.da and dd experimenttaly re-adjust the probability using adp_xtea_f_approx. p and dd.da.| A | transition probability matrices for 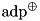 (adp_xor_sf). (adp_xor_sf). |
| AA | transition probability matrices for 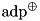 with FI (adp_xor_fixed_input_sf). with FI (adp_xor_fixed_input_sf). |
| key | round key. |
| delta | round constant. |
| da | input difference. |
| ret_dd | output difference. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
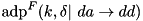
| double max_dx_adp_xtea_f | ( | const uint32_t | n, |
| uint32_t * | ret_dx, | ||
| const uint32_t | dy, | ||
| const uint32_t | key, | ||
| const uint32_t | delta, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const | ||
| ) |
For given output difference dy, compute the maximum probability input differences dx over all input differences: 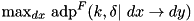 through exhaustive search over all input values and input differences. Complexity:
through exhaustive search over all input values and input differences. Complexity: 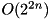 .
.
| n | word size. |
| ret_dx | maximum probability input difference. |
| dy | output difference. |
| key | round key. |
| delta | round constant. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
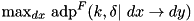 .
. | double max_dx_adp_xtea_f_exper | ( | uint32_t * | dx_max, |
| const uint32_t | dy, | ||
| const uint32_t | k, | ||
| const uint32_t | delta, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const | ||
| ) |
For given output difference dy, compute the maximum probability input differences dx over all input differences: 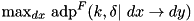 through exhaustive search over all input values and input differences. Complexity:
through exhaustive search over all input values and input differences. Complexity: 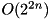 .
.
| dx_max | maximum probability input difference. |
| dy | output difference. |
| k | round key. |
| delta | round constant. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
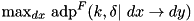 .
. | double max_dy_adp_xtea_f | ( | const uint32_t | n, |
| const uint32_t | dx, | ||
| uint32_t * | ret_dy, | ||
| const uint32_t | key, | ||
| const uint32_t | delta, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const | ||
| ) |
For given input difference dx, compute the maximum probability output difference dy over all output differences: 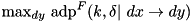 . Complexity:
. Complexity: 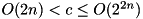 . Memory requirement:
. Memory requirement: 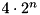 Bytes.
Bytes.
| n | word size. |
| dx | input difference. |
| ret_dy | maximum probability output difference. |
| key | round key. |
| delta | round constant. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
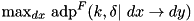 .
. | double max_dy_adp_xtea_f_exper | ( | const uint32_t | dx, |
| uint32_t * | dy_max, | ||
| const uint32_t | k, | ||
| const uint32_t | delta, | ||
| const uint32_t | lsh_const, | ||
| const uint32_t | rsh_const | ||
| ) |
For given input difference dx, compute the maximum probability output difference dy over all output differences: 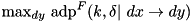 through exhaustive search over all input values and input differences. Complexity:
through exhaustive search over all input values and input differences. Complexity: 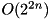 .
.
| dx | input difference. |
| dy_max | maximum probability output difference. |
| k | round key. |
| delta | round constant. |
| lsh_const | LSH constant. |
| rsh_const | RSH constant. |
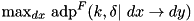 .
.