Header file for adp-tea-f-fk-noshift.cc:
More...
Go to the source code of this file.
| #define ADP_F_OP_NOSHIFT_COLSUM 2 |
Sum of the non-zero elements in one column of the F' matrices.
| #define ADP_F_OP_NOSHIFT_ISTATE 64 |
Initial state for start of the compuation of the ADP of F'.
| #define ADP_F_OP_NOSHIFT_MSIZE (1L << 7) |
Number of states of the S-function for F'.
| #define ADP_F_OP_NOSHIFT_NINPUTS 4 |
Number of inputs to F': 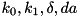 .
.
| #define ADP_F_OP_NOSHIFT_NMATRIX 32 |
Number of transition probability matrices for F'.
Normalization factor for transforming the elements of the matrices into probabilities.
Number of special positions for ADP of F'.
| double adp_f_op_noshift |
( |
gsl_matrix * |
A[NSPOS][2][2][2][2][2], |
|
|
uint32_t |
k0, |
|
|
uint32_t |
k1, |
|
|
uint32_t |
delta, |
|
|
uint32_t |
da, |
|
|
uint32_t |
db |
|
) |
| |
The additive differential probability (ADP) of a modified version of the F-function of TEA with the shift operations removed, denoted by F' and defined as:
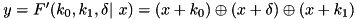 .
.
Complexity: 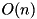 .
.
- Parameters
-
| A | transition probability matrices for 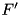 computed with adp_f_op_noshift_sf computed with adp_f_op_noshift_sf |
| k0 | first round key. |
| k1 | second round key. |
| delta | round constant. |
| da | input difference. |
| db | output difference. |
- Returns
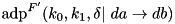 .
.
| void adp_f_op_noshift_alloc_matrices |
( |
gsl_matrix * |
A[NSPOS][2][2][2][2][2] | ) |
|
Allocate memory for the transition probability matrices for 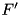 .
.
- Parameters
-
| A | transition probability matrices for 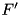 . . |
- See Also
- adp_rsh_xor_free_matrices
| double adp_f_op_noshift_exper |
( |
uint32_t |
k0, |
|
|
uint32_t |
k1, |
|
|
uint32_t |
delta, |
|
|
uint32_t |
da, |
|
|
uint32_t |
db |
|
) |
| |
The additive differential probability (ADP) of F' (a modified version of the F-function of TEA with the shift operations removed) computed experimentally over all inputs. Complexity: 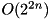 .
.
- Parameters
-
| k0 | first round key. |
| k1 | second round key. |
| delta | round constant. |
| da | input difference. |
| db | output difference. |
- Returns
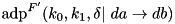 .
.
- See Also
- adp_f_op_noshift
| void adp_f_op_noshift_free_matrices |
( |
gsl_matrix * |
A[NSPOS][2][2][2][2][2] | ) |
|
Free memory reserved by a previous call to adp_rsh_xor_free_matrices.
- Parameters
-
| A | transition probability matrices for 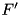 . . |
| void adp_f_op_noshift_normalize_matrices |
( |
gsl_matrix * |
A[NSPOS][2][2][2][2][2] | ) |
|
Transform the elements of A into probabilities.
- Parameters
-
| A | transition probability matrices for 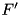 . . |
| void adp_f_op_noshift_print_matrices |
( |
gsl_matrix * |
A[NSPOS][2][2][2][2][2] | ) |
|
Print the elements of A.
- Parameters
-
| A | transition probability matrices for 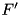 . . |
| void adp_f_op_noshift_sf |
( |
gsl_matrix * |
A[NSPOS][2][2][2][2][2] | ) |
|


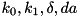 .
. 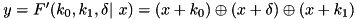 .
. .
. computed with adp_f_op_noshift_sf
computed with adp_f_op_noshift_sf 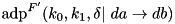 .
. 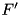 .
. 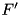 .
. 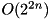 .
.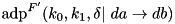 .
. 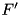 .
. 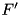 .
. 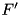 .
. 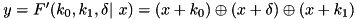 .
.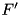 .
.![$A[j][2][2][2][2][2] = A[j][k0[i]][k1[i]][\delta[i]][da[i]][db[i]]$](form_98.png) , where
, where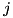 : dummy variable for future use.
: dummy variable for future use.![$k_0[i]$](form_99.png) : the i-th bit of the first round key.
: the i-th bit of the first round key.![$k_1[i]$](form_100.png) : the i-th bit of the second round key.
: the i-th bit of the second round key.![$\delta[i]$](form_101.png) : the i-th bit of the round constant:
: the i-th bit of the round constant:![$da[i]$](form_81.png) : the i-th bit of the input difference.
: the i-th bit of the input difference.![$db[i]$](form_102.png) : the i-th bit of the output difference.
: the i-th bit of the output difference.