YAARX: Yet Another ARX Toolkit  0.1
 All Data Structures Files Functions Variables Macros Pages
Functions | Variables
adp-arx.cc File Reference

The ADD differential probability of the sequence of operations: ADD, LROT, XOR (ARX): 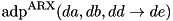$\mathrm{adp}^{\mathrm{ARX}}(da,db,dd \rightarrow de)$. More...

#include "common.hh"
#include "adp-arx.hh"

Functions

void adp_arx_alloc_matrices (gsl_matrix *A[2][2][2][2])
 
void adp_arx_free_matrices (gsl_matrix *A[2][2][2][2])
 
void adp_arx_normalize_matrices (gsl_matrix *A[2][2][2][2])
 
void adp_arx_print_matrices (gsl_matrix *A[2][2][2][2])
 
void adp_arx_sf (gsl_matrix *A[2][2][2][2])
 
double adp_arx (gsl_matrix *A[2][2][2][2], uint32_t rot_const, uint32_t da, uint32_t db, uint32_t dd, uint32_t de)
 
double adp_arx_exper (uint32_t r, uint32_t da, uint32_t db, uint32_t dd, uint32_t de)
 

Variables

uint32_t ADP_ARX_ISTATES [ADP_ARX_NISTATES] = {0,2,4,6}
 
uint32_t ADP_ARX_FSTATES [ADP_ARX_NISTATES][ADP_ARX_NFSTATES] = {{0,1}, {2,3}, {4,5}, {6,7}}
 

Detailed Description

The ADD differential probability of the sequence of operations: ADD, LROT, XOR (ARX): 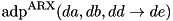$\mathrm{adp}^{\mathrm{ARX}}(da,db,dd \rightarrow de)$.

Author
V.Velichkov, vesse.nosp@m.lin..nosp@m.velic.nosp@m.hkov.nosp@m.@uni..nosp@m.lu
Date
2012-2013

Function Documentation

double adp_arx ( gsl_matrix *  A[2][2][2][2],
uint32_t  rot_const,
uint32_t  da,
uint32_t  db,
uint32_t  dd,
uint32_t  de 
)

The additive differential probability of ARX 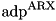$\mathrm{adp}^{\mathrm{ARX}}$. Complexity: $O(n)$.

Parameters
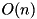Atransition probability matrices for 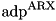$\mathrm{adp}^{\mathrm{ARX}}$ computed with adp_arx_sf.
rot_constrotation constant.
dafirst input difference (input to ADD).
dbsecond input difference (input to ADD).
ddthird input difference (input to XOR).
deoutput difference (output from ARX).
Returns
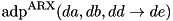$\mathrm{adp}^{\mathrm{ARX}}(da,db,dd \rightarrow de)$.
Note
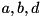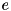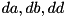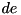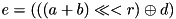If $a,b,d$ and $e$ are values that satisfy the differences $da,db,dd$ and $de$ respectively, then the ARX operation is defined as: $e = (((a + b) \ll< r) \oplus d)$.
void adp_arx_alloc_matrices ( gsl_matrix *  A[2][2][2][2])

Allocate memory for the transition probability matrices for 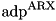$\mathrm{adp}^{\mathrm{ARX}}$.

Parameters
Atransition probability matrices for 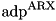$\mathrm{adp}^{\mathrm{ARX}}$.
See Also
adp_arx_free_matrices
double adp_arx_exper ( uint32_t  r,
uint32_t  da,
uint32_t  db,
uint32_t  dd,
uint32_t  de 
)

The additive differential probability of ARX ( 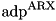$\mathrm{adp}^{\mathrm{ARX}}$) computed experimentally over all inputs. Complexity: $O(2^{4n})$.

Parameters
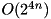rrotation constant.
dafirst input difference (input to ADD).
dbsecond input difference (input to ADD).
ddthird input difference (input to XOR).
deoutput difference (output from ARX).
Returns
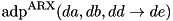$\mathrm{adp}^{\mathrm{ARX}}(da,db,dd \rightarrow de)$.
See Also
adp_arx
void adp_arx_free_matrices ( gsl_matrix *  A[2][2][2][2])

Free memory reserved by a previous call to adp_arx_alloc_matrices.

Parameters
Atransition probability matrices for 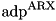$\mathrm{adp}^{\mathrm{ARX}}$.
void adp_arx_normalize_matrices ( gsl_matrix *  A[2][2][2][2])

Transform the elements of A into probabilities.

Parameters
Atransition probability matrices for 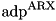$\mathrm{adp}^{\mathrm{ARX}}$.
void adp_arx_print_matrices ( gsl_matrix *  A[2][2][2][2])

Print the matrices for 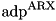$\mathrm{adp}^{\mathrm{ARX}}$.

Parameters
Atransition probability matrices for 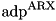$\mathrm{adp}^{\mathrm{ARX}}$.
void adp_arx_sf ( gsl_matrix *  A[2][2][2][2])

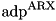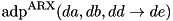S-function for $\mathrm{adp}^{\mathrm{ARX}}$: $\mathrm{adp}^{\mathrm{ARX}}(da,db,dd \rightarrow de)$.

Parameters
Azero-initialized set of matrices.
Returns
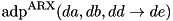Transition probability matrices A for $\mathrm{adp}^{\mathrm{ARX}}(da,db,dd \rightarrow de)$.

$A[2][2][2][2] = A[j][dc[i]][dd[i+r]][de[i+r]]$, where

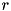  • $r$ : rotation constant.
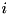  • $dc[i]$ : the $i$-th bit of the first input difference.
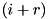  • $dd[i+r]$ : the $(i+r)$-th bit of the second input difference.
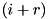  • $dd[i+r]$ : the $(i+r)$-th bit of the output difference.
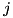  • $j$ : special bit postion:
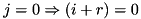    1. $ j = 0 \Rightarrow (i+r) = 0$.
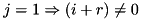    2. $ j = 1 \Rightarrow (i+r) \neq 0$.
Note
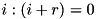At bit position $i: (i+r) = 0$, a special set of matrices is generated for which the carries generated at position 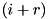$(i+r)$ in the differences 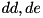$dd,de$ are set to 0.

Variable Documentation

uint32_t ADP_ARX_FSTATES[ADP_ARX_NISTATES][ADP_ARX_NFSTATES] = {{0,1}, {2,3}, {4,5}, {6,7}}

Array of final states for the S-function of 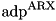$\mathrm{adp}^{\mathrm{ARX}}$: adp_arx_sf. Every set of final states corresponds to a unique initial state (ADP_ARX_ISTATES).

uint32_t ADP_ARX_ISTATES[ADP_ARX_NISTATES] = {0,2,4,6}

Array of initial states for the S-function of 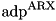$\mathrm{adp}^{\mathrm{ARX}}$: adp_arx_sf.